zadania z testu kwalifikacyjnego na studia Jo-anna: Witam! Zdawałam test na studia matematyczne, znam też już odpowiedzi typu TAK/ NIE, lecz wciąż ie mogę zrozumieć kilku zadań. Prosiłabym o jakąś wskazówkę do ich rozwiązania. 1. Czy w podanym zbiorze trójkątów istnieją trójkąty o dowolnie dużym polu a) zbiór trójkątów opisanych na okręgu o promieniu 1. b) zbiór trójkątów o obwodzie 1. [ co rozumieć pod nazwą dowolnie duże pole? odp na a−T, b− N, dlaczego?] 2. Czy w podanym zbiorze czworokątów istnieją czworokąty o dowolnie małym polu: a)zbiór prostokątów o przekątnych długości 1, T b)zbiór czworokątów opisanych na okręgu o promieniu 1 N c) zbiór rombów o bokach długości 1 T d)zbiór czworokątów wypukłych o obwodzie 1? T 3. Czy liczna nⁿ jest podzielna przez 2¹⁰⁰, jeżeli a) n=123 N b) n=82 N c) n=32 T d) n+52 T [ ad.a) coś podobno dlatego, ze podstawa nie jest parzysta, ale nie rozumiem, a w ad.b) że jest podzielna prze 2, ale nie przez 4...?]

	n k		n k+7
4. Czy równość		=		jest prawdziwa dla:

a) n=21 k=8 N b) n=49 k=21 T c) n=38 k=15 N d) n=27 k=10 T [miałam to wyliczyć bez kalkulatora, jak to zrobić? obiło mi się, ze n=2k+7, ale skąd to się wzięło?] 5. Czy istnieje taka liczba rzeczywista x> 2012, że 2^x>x²012 [odpowiedz brzmi tak, ale jak odpowiedzieć na to pytanie bez jakichkolwiek obliczeń?] 6. W turnieju wzięło udział 15 szachistów. Żadnych dwóch nie rozegrało ze sobą więcej niż jednej partii szachów. Czy jest możliwe, aby w czasie turnieju każdy z zawodników rozegrał: a) dokładnie 5 partii N b) dokładnie 9 partii N c) dokładnie 7 partii N d) dokładnie 6 partii? T Z góry dziękuję za poświęcony czas i pozdrawiam

Amaz: Przeciez zadanie 4 jest proste, czego nie wiesz? Wystarczy porównać, poskracać i zobaczyć czy to jest to samo. Przykład a:

21!		21!		1		1
	=		⇒		=		⇒
8!13!		15!6!		8!		6!*14*15

	1		1
⇒		=		, tutaj już chyba jasno widać, że równość prawdziwa nie jest.
	7*8		14*15

Tomek.Noah:

	n k
z 4 chodzi o to że w dwumianach jest pewien trik a mianowicie ze wyrazy		co do wartosci

	n n−k
jest rowna dwumianowi		i tak chyba najszybciej sie da znalesc bez kalkulatora

Tomek.Noah: w 5 choćby nawet 0 jak sobie podstawisz

Tomek.Noah: wróć nie zauważyłem warunku xD

Amaz: To prawda Tomek.Noah, ale takie rzeczy powinno się samemu zauważać.

ICSP: 0 > 2012 ?

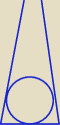
Godzio: Zad. 1 Obwód jest ograniczony, pole od niego zależy więc również jest ograniczone Jeśli chodzi o trójkąt opisany na trójkącie, patrz rysunek − jeśli ramiona będą prawie pionowe to będzie dowolnie duże pole

Tomek.Noah: co do 5 to dziwne bo jak mam x>2012 2^x>x²⁰¹² log₂2^x>log₂x²⁰¹² x>2012*log₂x gdzie x>2012 to log₂x jest wieksze od jedynki więc sprzeczność

Godzio: Zad. 2 82 = 2 * 41 (2 * 41)⁸² = 2⁸² * 41⁸², a 2⁸² nie dzieli 2¹⁰⁰ analogicznie reszta

Amaz: Godzio chodzisz na wyklady A czy B?

Godzio: B

Amaz: Jak chcesz to mam na kompie skany starych kartkówek i kół z wdm B

Godzio: Nie trzeba, mam tego ful ze strony wykładowcy i do części są rozwiązania więc spoko

Amaz: Ok, jakbyś czegoś potrzebował, to Ci pomogę w miarę możliwości.

Godzio: Ok Będę pamiętać