wartość bezwzględna PuRXUTM: IIx−2I+xI=4 IIx−2I+xI=4 ⇔ Ix−2I +x=4 v Ix−2I +x=−4 interesuje mnie takie przejście Ix−2I +x=−4 Ix−2I=−4−x to jest chyba sprzeczność, ale dlaczego ?

Saizou : nie jest sprzecznością bo nie znasz "x", a gdyby x=−5

Piotr: a przenies sobie wszystko na lewo

PuRXUTM: ale wychodzą mi jakieś głupoty że x =−1 a podstawiając nie pasuje( chyba że się gdzieś pomyliłem )

Patryk: |x−2|=t

Patryk: ale to nie zadziała bo tam jest x a nie liczba eh

PuRXUTM: ale Patryk co mi to da ? spróbuj przeliczyć tak jak ja z def. bo ja liczę i ciągle wychodzi to samo

Piotr: patrzac na to : |x−2|+x = −4 wiemy ze x musi byc ujemny bo inaczej nie ma szans zeby wyszlo −4. tylko ze kiedy x bedzie ujemny to wartosc bezwzgledna |x−2| bedzie wieksza od od samego x. rownanie sprzeczne.

PuRXUTM: no w sumie tak dzięki wielkie o to mi chodziło, strasznie trzeba myśleć przy tych zadaniach

Saizou : a może w przedziałach x∊(−∞:0> (0:2) <2:+∞)

Eta: |x−2|+x= 4 lub |x−2|+x= −4 dla x≥2 x−2+x=4 lub x−2+x= −4 x= 3 lub x= −2 −− odpada podobnie dla x<2 dokończ .....

pigor: ... , np. tak : szukamy rozwiązań danego równania x=? takich, że ||x−2|+x|= 4 ⇔ |x−2}+x=4 ∨ |x−2|+x= −4 ⇔ ⇔ (|x−2|= −x+4 ∧ −x+4 ≥0) ∨ (|x−2|= −x−4 ∧ −x−4 ≥0) ⇔ ⇔ (x−2= −x+4 ∧ −x+4 ≥0) ∨ (x−2= −x−4 ∧ −x−4 ≥0) ⇔ ⇔ (2x=6 ∧ x≤ 4) ∨ (2x= −2 ∧ x≤ −4) ⇔ (x=3 ∧ x≤ 4) ∨ (x= −1 ∧ x≤ −4) ⇔ ⇔ x=3 ∨ x∊∅ ⇔ x=3 . .,..

PuRXUTM: no w sumie przedziałami najlepiej dzięki

PuRXUTM: pigor za bardzo twojego rozumowania nie rozumiem ale to norma

Eta:

Piotr: trzeba sie wczytac !

pigor: ...cóż ja używam podstaw logiki , czyli alternatywy koniunkcji albo koniunkcji alternatyw i wszystko .. często wychodzi na końcu samo .

PuRXUTM: wiem wiem ale mój mózg pewnych operacji pojąć nie może

Mila: Napisałam graficzny sposób, ale komputer zawiesił się. Spróbuję jeszcze raz.

Saizou : ja na początku jak to zobaczyłem nie mogłem zrozumieć dlaczego została opuszczona druga wartość bezwzględna (tu) (|x−2|= −x+4 ∧ −x+4 ≥0) ∨ (|x−2|= −x−4 ∧ −x−4 ≥0) i w końcu doszedłem do wniosku że założenie −x+4≥0 oraz −x−4≥0 wynika z def. wartości bezwzględnej, dobrze myślę

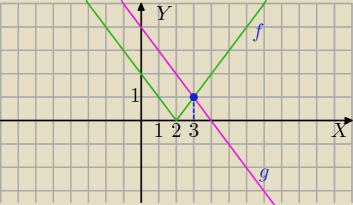
Mila: (a) Ix−2I +x=4 v (b) Ix−2I +x=−4 (a) f(x)=|x−2| g(x)=−x+4 x=3 z odczytu Jeśli nie można dokładnie odczytać to rozwiązujesz równanie: −x+4=x−2 6=2x x=3 Sam wykonaj przykład (b)

Piotr: dobrze myslisz Saizou

Saizou : dziękuję bardzo za potwierdzenie, bo ta metoda jest bardzo ciekawa

PuRXUTM: Mila dzięki za fatygę ale nie chcę tego rozwiązywać na 1001 sposobów wystarczy mi jeden z przydziałami podany przez Etę, ten Pigora to wyższa szkoła jazdy

Eta: Metoda graficzna niekiedy zawodzi

	3
Co by było, gdyby rozwiązaniem był x=
	11

Piotr: głosuję na sposób pigora

Saizou : I like it Piotr

sdfgh\: karny