Liczby zespolone prosze: Liczby zespolone. Witajcie. Mam do rozwiązania (1−i)⁷ . Jak to obliczyć? Bo mi nic nie wychodzi. Dziękuję!

ZKS: Zamień na postać trygonometryczną.

Mila: (1−i)²=1−2i+i²=−2i rozpisz (1−i)⁷ i skorzystaj z tego co policzyłam

prosze: Oczywiście, że zamieniłem ale mam sinus −√2/2 i cosinus p{2)/2 i nie mogę znaleźć kąta. Z innymi zadaniami nie miałem problemu, z tym tak.

ICSP: a w której ćwiartce sinus jest ujemny a cosinus dodatni ?

prosze: W czwartej, czyli II − II/4?

ICSP:

	π
2π −		=
	4

prosze: To znaczy 2π−^π₄?

prosze: Ok, to już obliczyłem, a czy dobry mam moduł? Mój moduł to √2.

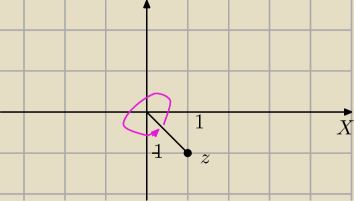
Mila: z=1−i Teraz widzisz kąt?

ICSP: Moduł

Mila: (1−i)⁷=[(1−i)²]³*(1−i)=(−2i)³*(1−i)=−8*i³*(1−i)= =8i*(1−i)=8i−8*i²=8+8i

prosze: Jak to zatem rozwiązać trygonometrycznie? Gdzie mnożymy kąty *7?

prosze: Ok, już rozumiem i inne przykłady też mi metodą mnożenia wyszły. Dzięki!

Mila: (1−i)⁷=√2⁷*(cosΦ+isinΦ)⁷=√2⁷*(cos7Φ+isin7Φ)

prosze: Bardzo dziękuję! Dłuższa przerwa i czasami się zapomina o najprostszych metodach.

Mila: Z postacią trygonometryczną też zrób, bo zapomnisz, a czasem trzeba.