prosze o pomoc
natalia: Istnieje taka liczba rzeczywista a, że układ równań:
x2=y2
(x−1)2+y2=a2
jest spełniony przez
A. dokładnie jedną parę liczb rzeczywistych (x, y)
B. dokładnie dwie pary liczb rzeczywistych (x, y)
C. dokładnie cztery pary liczb rzeczywistych (x, y)
D. dokładnie pięć par liczb rzeczywistych (x, y)
4 paź 14:55
natalia: pytanie jest wielokrotnego wyboru
4 paź 14:58
Basia: rozwiąż ten układ; po rozwiązaniu natychmiast będzie wiadomo, która odpowiedź jest poprawna
4 paź 15:00
natalia: x2−2x+1+x2=a2
2x2−2x+1=a2
co musze robic dalej?
4 paź 15:02
natalia: 
4 paź 15:11
Basia:
(x−1)2+x2=a2
x2−2x+1+x2−a2=0
2x2 −2x + (1−a2)=0
Δ = 4 − 8(1−a2) = 8a2−4 = 8(a2−12)
i teraz:
1. dla tych a, dla których Δ=0 może być jedna para dla x0=0 bo wtedy y2=02=0 czyli y=0 i
masz parę (0;0) lub dwie pary jeżeli x0≠0 bo wtedy y=±x0 i masz pary (x0;x0) i (x0; −x0)
2. dla tych a, dla których Δ>0 możesz mieć: trzy pary jeżeli x1=0 i x2≠0 (lub odwrotnie) lub
cztery pary jeżeli x1≠0 i x2≠0
D raczej nie uda się uzyskać a to co napisałam trzeba teraz policzyć
bo trzeba zbadać czy opisane przypadki są możliwe
4 paź 15:11
Basia: jeżeli to nie jest dość jasne pytaj dalej
4 paź 15:12
Basia: ciekawe są te zdania; możesz napisać z jakiego są zbioru ?
4 paź 15:19
Mila:
Dołożę do Basi wyjaśnień ilustrację.
Rozważę przypadek, gdy jeden z pierwiastków równania:
2x
2 −2x + (1−a
2)=0
jest równy 0.
Wówczas 1−a
2=0⇔a=1 lub a=−1
mamy:
2x
2−2x=0
x(2x−2)=0⇔x=0 lub x=1
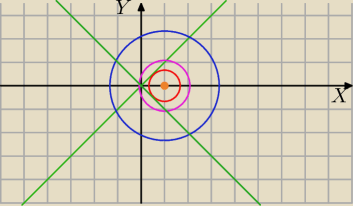
(0,0) (1,1)(1,−1) trzy rozwiązania różowy okrąg
Ilustracja graficzna:
x
2−y
2=0⇔
(x−y)(x+y)=0⇔x−y=0 lub x+y=0⇔y=x lub y=−x
Czerwony okrąg styczny do prostych: 2 rozwiązania
Niebieski okrąg:4 rozwiązania
4 paź 18:14

 Dołożę do Basi wyjaśnień ilustrację.
Rozważę przypadek, gdy jeden z pierwiastków równania:
2x2 −2x + (1−a2)=0
jest równy 0.
Wówczas 1−a2=0⇔a=1 lub a=−1
mamy:
2x2−2x=0
x(2x−2)=0⇔x=0 lub x=1
(0,0) (1,1)(1,−1) trzy rozwiązania różowy okrąg
Ilustracja graficzna:
x2−y2=0⇔
(x−y)(x+y)=0⇔x−y=0 lub x+y=0⇔y=x lub y=−x
Czerwony okrąg styczny do prostych: 2 rozwiązania
Niebieski okrąg:4 rozwiązania
Dołożę do Basi wyjaśnień ilustrację.
Rozważę przypadek, gdy jeden z pierwiastków równania:
2x2 −2x + (1−a2)=0
jest równy 0.
Wówczas 1−a2=0⇔a=1 lub a=−1
mamy:
2x2−2x=0
x(2x−2)=0⇔x=0 lub x=1
(0,0) (1,1)(1,−1) trzy rozwiązania różowy okrąg
Ilustracja graficzna:
x2−y2=0⇔
(x−y)(x+y)=0⇔x−y=0 lub x+y=0⇔y=x lub y=−x
Czerwony okrąg styczny do prostych: 2 rozwiązania
Niebieski okrąg:4 rozwiązania