jak to zrobic ? Ala: Udowodnij ze jezeli P((A'∪B)∩A)≥¹₆ to P(A')=¹₃ i P(B')=¹₂

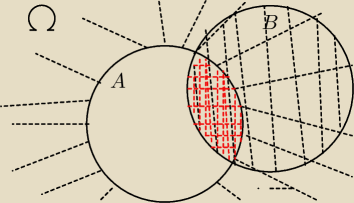
imię lub nick: doszedłem do tego, że: P(A∩B)=P((A'∪B)∩A) ale co dalej... nie mam pojęcia.

@Basia: Wydaje mi się, że to nieprawda, bo: tak jak napisał imię lub nick P((A'∪B)∩A) = P(A∩B) = P( (A'∪B'))' = 1−P(A'∪B') jeżeli: 1−P(A'∪B') ≥¹₆ ⇒ 1−¹₆ ≥ P(A'∪B') czyli: P(A'∪B')≤⁵₆ P(A'∪B') = P(A')+P(B')−P(A'∩B') ≤ ⁵₆ ¹₃+¹₂ − P{A'∩B') ≤ ⁵₆ P(A'∩B') = 0 a tak przecież być nie musi może oczywiście, ale nie musi Alu sprawdź czy wszystko na pewno dobrze napisałaś

Jakub: ¹₃ + ¹₂ − P(A'∩B') = ²₆ + ³₆ − P(A'∩B') = ⁵₆ − P(A'∩B') ≤ ⁵₆ ponieważ P(A'∩B') ≥0 @Basia tam w tej nierówności P(A'∩B') odejmujesz a nie dodajesz, czyli lewa strona w najgorszym przypadku okaże się równa ⁵₆

Ala: tak wszystko dobrze napisałam