trygometria monia41: dla kata alfa w trojkacie prostokatnym wiemy ze tg alfa=2 oblicz wart.pozostałych funkcjitrygometrycznych

Artur_z_miasta_Neptuna: skoro tgα = 2 to:

	1		1
1) ctgα =		=
	tgα		2

	sinα
2) tgα =		= 2 ⇔ sinα = 2cosα
	cosα

3) skorzystaj z 'jedynki trygonometrycznej' sin²α + cos²α = 1 //podstaw z punktu 2// (2cosα)² + cos²α = 1 4cos²α + cos²α = 1 5cos²α = 1

	1
cos2α =
	5

	1		√5
cosα =		=		// cosinus jest dodatni dla kątów ≤90o a tylko takie występują
	√5		5

w trójkącie prostokątnym // 4)

	√5		√5		2√5
skoro cosα =		to sinα = 2cosα = 2		=
	5		5		5

przeanalizuj i zapamiętaj tok myślenia

Aga1.: Można inaczej

	a		2
tgα=		=		⇒ a=2x, b=x
	b		1

Z twierdzenia Pitagorasa c²=a²+b² c²=x²+(2x)² c²=5x² c=√5x

	b		x		1		√5
cosα=		=		=		=
	c		√5x		√5		5

	a
sinα=		=
	c

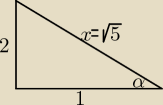Bogdan: Dopuszcza się w egzaminach maturalnych nawet takie, trochę nieformalne rozwiązania: x = √2¹ + 1² = √5

	2
sinα =
	√5

	1
cosα =
	√5