? Patryk: Zaznacz w układzie wsp zbiór A={(x,y): |y−2x+3|≤1} jak ?

Basia: |y−2x+3| ≤ 1 ⇔ −1 ≤ y−2x+3 ≤ 1 ⇔ 2x−4 ≤ y ≤ 2x − 2 ⇔ y≥ 2x−4 i y≤ 2x−2 teraz rysuj

Patryk: więc można sobie przyjąć ,ze t=y−2x+3 no i później wrócić do t ?

Basia: oczywiście ogólniej: |wyrażenie| ≤ a ⇔ −a ≤ wyrażenie ≤ a wyrażenie może być jakie tylko chcesz

Patryk: dzięki bardzo

Patryk: a jeszcze y<−3x−2 i y>−3x+2 ,to zbiór pusty ?

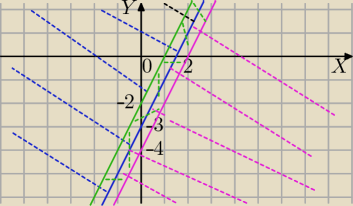
Mila: 1) y−2x+3≥0⇔y≥2x−3 rysuję prostą i zaznaczam punkty powyżej tej prostej (niebiesko!) − w tej dziedzinie mamy nierówność: y−2x+3≤1 ⇔ y≤2x−2 punkty poniżej tej prostej w obszarze niebieskim 2)y−2x+3<0⇔y<2x−3 obszar poniżej tej prostej (różowy) − w tej dziedzinie mamy nierówność: −y+2x−3≤1 ⇔−y+2x−4≤0 ⇔y≥2x−4 punkty powyżej tej prostej w obszarze różowym Zbiór A to punkty leżące w pasie między prostymi ; y=2x−2 i y=2x−4

Basia: tak

Patryk: dzieki MIla

Basia: odpowiedź do wpisu z 21:26 brzmi: tak

Patryk: ok

Patryk: B={(x,y): |y+3x|>2} dlaczego tu jest suma ,czyli (−2>y+3x U y+3x>2)

Patryk: przypuszczam ,ze chodzi tu o znak nierówności ale nie wiem dlaczego

Patryk: ?

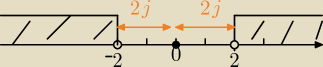
Mila: |a|>2⇔a<−2 lub a>2 odległość na osi od zera jest większa niż 2 jednostki