| √3 | ||
wytlumaczeniem postepowania.Wynik P= | s2 | |
| 8 |
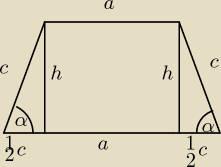α = 60o
zauwaz ze po zlaczeniu tych dwoch trojkatow wyjdzie trojkat rownoramienny gdzie h= c√32
do wzoru na pole potrzebujemy → podstawy dolnej, podstawy gornej i wysokosci
podstawa dolna = c+a
podstawa gorna = a
wysokosc trapezu = c√32 mamy troche za duzo danych
ramie trapezu = c
bylo powiedziane ze obwod to 2s czyli 2s = c+a+a+2c 2s=3c+2a 2a = 2s−3c
a=2s−3c2a
czyli podstawa dolna to c+ 2s−3c2
a gorna to 2s−3c2
teraz podstawiamy to wszystko do wzoru na pole
P= 12 ( 2s−3c2 + 2s−3c2 +c ) * c√32
po przemnozeniu wszystkiego wychodzi P = −12c2√3 + 12cs√3
Δ= 34 s2
| −34 s2 | ||
Pmax = −Δ4a = | = √38 s2
| |
| −2√3 |
