k mrrr: Sprowadzam liczbę zespoloną w postaci a + bi do postaci trygonometrycznej. z = −3 + 3i |z| = √18 = 3√2

	−3		−1		√2
cosδ =		=		= −
	3√2		√2		2

	3		√2
sinδ =		=
	3√2		2

Teraz mam problem, jak najłatwiej ustalić taki kąt?

	π
Z interpretacji geometrycznej widzę, że kąt leży w I ćwiartce − δ ∊ (0,		) ale nie bardzo
	2

wiem jak go ustalić. Jeszcze jedno − czymże się różni argument od argumentu głównego? Mogę prosić o jakiś przykład bo nie mogę zapałać.

mrrr: Przepraszam, oczywiście się pomyliłem δ ∊ (0, π).

Krzysiek: najłatwiej argument można wyczytać z rysunku, zaznacz liczbę 'z' na płaszczyźnie zespolonej http://pl.wikipedia.org/wiki/P%C5%82aszczyzna_zespolona

	π		π
wtedy widać, że δ=		+
	2		4

mrrr:

	3π
Dziękuję za odpowiedz, jednak nie mogę się doczytać skąd można obliczyć, ze δ =		.
	4

Krzysiek:

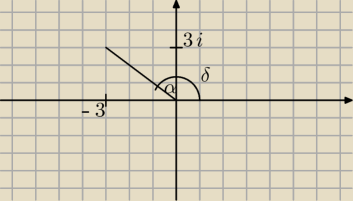
	3		π
czyli: tgα=		=1 ⇒α=
	3		4

	π		π
więc: δ=		+
	4		2

MQ: δ nie leży w I ćwiartce, chociażby dlatego, że cosδ jest ujemny.

	π
Leży w II ćwiartce: δ∊(		,π)
	2

mrrr: Myli mi się to jeszcze ale pracuję nad tym . Krzysiek − chyba już rozumiem, dziękuję. Czy dobrze obliczyłem, że liczbę −3 + 3i można przedstawić jako:

	3π		3π
z = 3√2 [cos(		+ 2kπ) + isin(		)]
	4		4

?

Krzysiek: ok, tylko po co to 2kπ?

mrrr: Tak nam na wykładzie kazała prowadząca pisać. Wszystkie zadania liczymy z tym okresem. Jednej rzeczy nie rozumiem, widzę z notatek, że prócz obliczenia przykładowo kąta między osia Re a półprostą przechodzącą przez pkt reprezentujący liczbę zespoloną liczymy jeszcze coś − tj. jakiś innych kąt, zdaje się, że dla np. I ćwiartki β = δ, dla II π − δ dla III π+δ dla IV 2π−δ. Czy to będzie ten argument?

mrrr: Własnie nie mogę pojąc czy we wzorze z = |z|[cosδ + isinδ], δ to kąt między półprostą a osią Re/OX to argument czy argumentem jest 2π−δ.

Krzysiek: jeżeli piszesz to 2kπ to chyba przy sinusie też powinno być...? co do Twojego pytania... to zapewne to samo robicie co ja teraz.. np. jakbym policzył miarę kąta 'pod' α (który tyle samo wynosi)nazwijmy go kątem β, to wtedy

	3π
argument wynosiłby δ=π−β=π−π/4 =
	4

mrrr: Tak, przy sinusie też powinno być. Po prostu nie mogę zrozumieć co się dzieje bo raz liczymy kąt między półprostą a raz różnicę π − δ itp. Przykładowo dla:

	3		1		π		π
−		+		i otrzymuję cos(		+ 2kπ )+ isin(		+ 2kπ) a na zajęciach wynik
	2		2		6		6

wyszedł:

	5π		5π
cos(		+ 2kπ) + isin(		+ 2kπ) czyli znów jakaś różnica − odjęli od π − δ nie wiem
	6		6

jak mam to liczyć.

Krzysiek: nie powinno być −√3{2} +1/2 i ? wtedy wynik na zajęciach jest ok... Liczysz tak samo jak ja wyżej..., liczysz kąt 'α' i dodajesz π/2

Krzysiek:

	−√3		1
"nie powinno być:		+		i "
	2		2

mrrr: Tak, z pierwiastkiem. Tylko nadal nie rozumiem dlaczego to odejmowanie czy we wzorze: |z|[cosδ + isinδ], δ to w końcu jaki kąt? Kąt między osią OX a a półprostą przechodzącą przez (Rez, Imz) czy 2(?)π(?) − kąt między półprostą a OX?

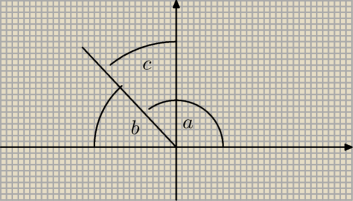
ania: δ to kąt zaznaczony jako a a= 90+c lub a=180−b do wyboru

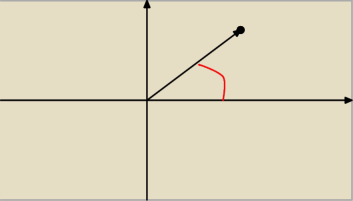
mrrr: We wzorze na postać tryg. podstawiam wartość czerwonego kąta czy innego?

mrrr: Ok, Ania. Czy z tego wynika, że w I ćwiartce za δ = α, w II π−α w III π+α IV 2π−α?

ania: tak