2 paź 17:55
Magda: x2−4x=4 = (x−2)2 ≥0
miejsce zerowe jest jedno ktore wynosi 2. jest to wierzcholek funkcji. funkcja jest dodatnia a
wiec ramiona sa skierowane do gory. reszte sam odczytasz z rysunku
2 paź 17:58
Magda: x2−4x+4 = (x−2)2 ≥0
2 paź 17:59
ania: obliczam deltę b2−4ac
Δ=16−4*1*4
Δ=0
x0=−b/2a
x0=4/2=2
rysujesz wykres. gdzie pierwiastkiem tej nierówności jest liczba 2 i piszesz rozwiązanie
2 paź 18:00
asdf: x2 = a = 1
Δ = 0 i jest nierówność ≥ 0
Z tego można już zauważyć, że x ∊ ...
2 paź 18:01
NIE UMIEM: no właśnie tego nie wiem że x należy ? x∊ (0,+
∞)
?
2 paź 18:05
asdf: nie
2 paź 18:06
NIE UMIEM: no to jak w końcu?
2 paź 18:08
Magda: masz tam znak wieksze badz ROWNE zeru. takze zero tez bierzesz pod uwage.
x∊<0,+∞)
2 paź 18:08
asdf:
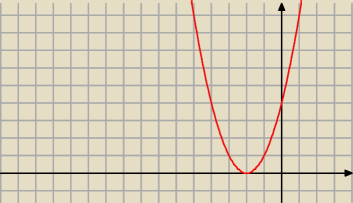
Tak wygląda ta funkcja, masz wyznaczyć przedział, które 'iksy' są nie ujemne, czyli ≥ 0
2 paź 18:08
asdf: @Magda
NIE!
2 paź 18:09
asdf: @Magda
Nie!
2 paź 18:09
Magda: pomylilam ze zbiorem. faktycznie...
2 paź 18:14
2 paź 18:16
NIE UMIEM: czyli od <2,+∞) jak nie tak to już nie wiem, matematyka ssie
2 paź 18:16
asdf: Chyba
ale nie mam czasu
2 paź 18:17
asdf: @NIE UMIEM
KAŻDY X PODNIESIONY DO KWADRATU NIE JEST LICZBĄ UJEMNĄ W ZBIORZE LICZB RZECZYWISTYCH
teraz udziel odpowiedzi
@Magda
Chyba, ale nie mam czasu, sorry
2 paź 18:18
Magda: @ nie umiem
bierzesz pod uwage to co jest nad osia x, a os x jest to os pozioma. wszystko jest nad nia.
wiec rozwiazaniem sa wszystkie liczby czyli (−∞,+∞) czyli R
@asdf
blagam, bo ja tego nie ogarniam
2 paź 18:19
rolnik :): masz rozwiązać x2−4x+4≥0 czyli znaleźć takie "iksy" dla których wartości są większe lub równe
zero, jak narysował @asdf − z tego odczytujemy że x2−4x+4≥0 dla x∊R
2 paź 18:20
NIE UMIEM: już rozumiem, dziękuję wszystkim !
2 paź 18:21
