zad
Aga: Niech A={ (x,y) : y ≥ ||x−2| − 1|}, B={ (x,y) : y + √4x − x2 − 3 ≤ 2 }. Narysować na
płaszczyźnie zbiór A∩B i obliczyć jego pole.
2 paź 08:57
Aga1.:
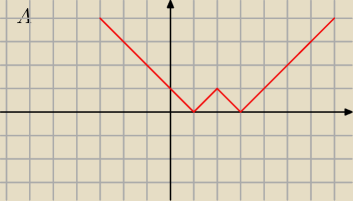
:
2 paź 09:58
Aga1.:
B
√−x2+4x−3≤2−y
Gdy −x2+4x−3≥0 i 2−y≥0
To można podnieść nierówność obustronnie do kwadratu
(2−y)2≥−x2+4x−3
2 paź 10:05
Aga: ale co dalej z tym zrobic

?
2 paź 10:17
Aga1.: Po przeniesieniu na lewą stronę otrzymasz okrąg i jego część zewnętrzną
B
narysuj wyznaczając część wspólną tych trzech nierówności
2 paź 10:30
ania: po pierwsze żeby pierwiastek istniał x ∊ (1;3)
potem podstawiać różne x i rysować
2 paź 10:33
ania:
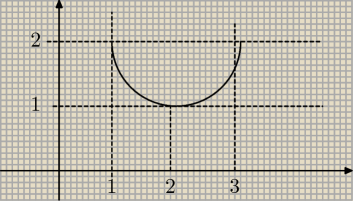
2 paź 10:37
ania: trochę te półkole za duże ale z grubsza widać ;>
2 paź 10:38
ania: no i y ≤ 2− √4x−x2−3 czyli to przestrzeń pod tym półkolem
2 paź 10:39
ania:
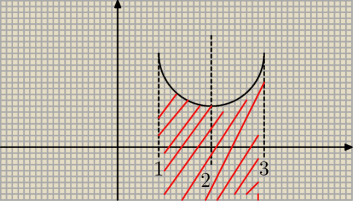
2 paź 10:42
Aga1.:
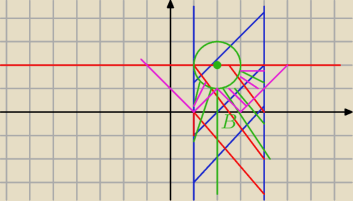
Mogłam się gdzieś pomylić.
2 paź 10:45
 :
:
 ?
?


 Mogłam się gdzieś pomylić.
Mogłam się gdzieś pomylić.