wspolrzedne anmi0op: Witam Prosze o pomoc Mając dany punkt przecięcia przekątnych w kwadracie S (−5,3) oraz współrzędne jednego z wierzchołków C (−3,7) podaj wspolrzedne pozostalych wierzcholkow tego kwadratu. Obliczyłam A=(−7,−1) z wektorow i stanelam w miejscu, co dalej?

anmi0op: prosze

loitzl9006: Nie będzie to chyba najprostszy pomysł, ale nie wiem jak prościej to rozwiązać. Skorzystaj z tego, że wektor SA ma być prostopadły do wektora SD. → SA = [ −2 ; −4 ] → SD = [ x_D+5 ; y_D−3 ] iloczyn skalarny wektorów SA i SD ma być równy zero, więc z tego masz równanie: −2*(x_D+5)−4(y_D−3)=0 pozostaje jeszcze uzależnić y_D od x_D. Można to zrobić poprzez wyznaczenie równania prostej SD: y=f(x). Prosta SD jest prostopadła do prostej SC (wykorzystaj warunek prostopadłości prostych), wyznaczonej przez dwa punkty S i C, i do prostej SD należy punkt S. Jak już będziesz mieć f(x) czyli wzór prostej SD, to współrzędne punktu D będą takie: (x_D, f(x_D)). Te obie współrzędne będą zależeć tylko od x_D, a więc wcześniejsze równanie z dwoma niewiadomymi x_D i y_D będzie można rozwiązać. Po znalezieniu współrzędnych x_D i y_D znajdujesz współrzędne B.

anmi0op: uff dziękuję za wyczerpująca odpowiedź, jutro to ogarnę i dam znać jak tam

dero2005: liczę współczynnik kierunkowy prostejSC

	yC−yS		7−3
aSC =		=		= 2
	xC−xS		−3−(−5)

liczę równanie prostej CS y_CS = a_CS(x − x_C) + y_C = 2x + 13 licze współczynnik kierunkowy prostej CD

	aSC−aCD
tgα = |		| = 1
	1+aSC*aCD

	1
aCD = aAB =
	3

	1
aCB = aAD = −		= −3
	aCD

liczę równanie prostej CD

	1
yCD = aCD(x − xC)+yC =		x + 8
	3

liczę równanie prostej CB y_CB = a_CB(x − x_C)+y_C = −3x − 2 liczę współczynnik kierunkowy prostej BD

	−1		1
aDB =		= −
	aSC		2

liczę równanie prostej DB

	1		1
yDB = aDB(x − xS)+ ys = −		x +
	2		2

szukam punktu D (porównuję proste CD i BD)

	1		1		1
−		x +		=		x + 8
	2		2		3

x = −9 y = 5 szukam punktu B (porównuje równania prostych BC i BD)

	1		1
−3x − 2 = −		x +
	2		2

x = −1 y = 1 licze równanie prostej BA

	1		4
yBA = aBA(x − xB) + yB =		x +
	3		3

szukam punku A (porównuje równania prostych AB i CS)

1		4
	x +		= 2x + 13
3		3

x = −7 y = −1 A (−7 , −1) B (−1 , 1) D (−9 , 5)

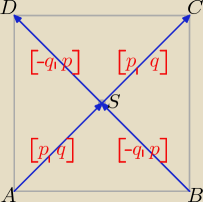
Bogdan: S = (−5, 3), C = (−3, 7). → SC = [2, 4], p = 2, q = 4, → AS = [2, 4], x_A + 2 = −5 ⇒ x_A = −7, y_A + 4 = 3 ⇒ y_A = −1, A = (−7, −1) → SD = [−4, 2], x_D = −5 − 4 = −9, y_D = 3 + 2 = 5, D = (−9, 5) → BS = [−4, 2], x_B − 4 = −5 ⇒ x_B = −1, y_B + 2 = 3 ⇒ y_B = 1, B = (−1, 1)

Eta:

loitzl9006: tym moim sposobem dojdziesz do tego, że 0=0. Zapomniałem o warunku, że długość wektora SA (a więc i odcinka SA) ma być równa długości odcinka SD. Zadanie można też rozwiązać, wyznaczając równanie prostej SC, potem równanie okręgu o środku w punkcie S i promieniu równym długości odcinka SC, a potem równanie prostej SD (⊥ do SC i przechodzącej przez punkt S). Następnie rozwiązujesz układ równań złożony z równania okręgu i równania prostej SD. Rozwiązanie tego układu to współrzędne B i D (punktów przecięcia prostej i okręgu). Można też tak: wyznaczyć równanie prostej SC w postaci ogólnej, potem wyliczyć długość |SC| (połowa przekątnej kwadratu ABCD), i zauważyć że |SC|=|DS|=|BS|. Punkty B i D będą równooddalone od prostej SC. Wykorzystaj wzór na odległość punktu D(x_D,y_D) od prostej SC. Wstaw wszystkie dane do tego wzoru, otrzymasz równania dwóch prostych: k i l, których odległość od prostej SC będzie równa |SC|=2√5. Wyznacz teraz równanie prostej SD. Następnie rozwiąż układ równań złożony z równania prostej SD i prostej k (rozwiązaniem będą współrzędne punktu B), potem układ równań z prostej l i prostej SD (współrzędne D).

Ann: dziękuje za tyle odpowiedzi straszne jest to zadanie dla mnie zatrzymałam się na liczeniu współczynnika kierunkowej prostej CD z postu dero2005 i nie wiem czemu jest tak a nie inaczej? skad to się wzięło?

Aga1.: Zastosuj sposób Bogdana ,jest najprostszy, gdyż jak wspomniałaś wiesz coś o wektorach.

Ann: tylko właśnie w odpowiedziach z arkusza jest zrobione sposobem dero2005, ale faktycznie zrobię to tym sposobem Bogdana, bo nie rozumiem za bardzo tamtego

Ann: zrobione!