Prosze o pomoc , kompletnie niewiem jak to wykonać
wixik: Witam , chciałby prosić o pomoc ponieważ mam 3 zadanie których nie potrafie zrobić , one są z
książki z jednego działu a mimo to i tak nie wiem jak je zrobić , mianowicie :
1 zad
Na przedłużeniu przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punkt D tak ,że
|BD|=|BC|. Oblicz |CD| , jeśli wiadomo że |BC| = 15 i |AC| = 8.
2 zad
Wyznacz długość boku c trójkąta, jeśli dane są długości a,b dwóch jego boków oraz wiadomo , że
ha + hb = hc , gdzie ha , hb, hc są długościami wysokości opuszczonych na odpowiednie
boki tego trójkąta.
3 zad
W trójkącie równoramiennym o polu 48 cm2 stosunek długości ramienia do długości wysokości
opuszczonej na podstawę jest równy 5:4. Oblicz obwód trójkąta , długość wysokości tego
trójkąta
1 paź 20:32
PuRXUTM: miałeś coś takiego jak twierdzenie cosinusów sinusów ?
1 paź 20:41
PuRXUTM: pierwsze mi wyszło 29,1 ( w przybliżeniu ) sprawdź w odpowiedziach ale jak nie miałeś
cosinusów i sinusów to nie napisze ci jak to robiłem bo nie będziesz raczej wiedział o co
chodzi
1 paź 20:51
wixik: miałem twierdzenie sinusów i cosinusów
2 paź 07:31
ania: 1 można z podobieństwa trójkątów ;>
2 paź 08:21
ania:
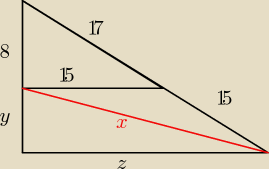
2 paź 08:23
ania: 17 oczywiście z pitagorasa
i z pitagorasa x
2 paź 08:25
ania: zad 2
z pól ale skróciłam dwójki w mianowniku w pamieci

h
a * a = h
b * b = h
c *c
h
a * a = h
b * b
h
b * b = h
c *c
h
b * b = ( h
a + h
b )*c
| | b | |
hb * b = ( hb * |
| + hb )*c |
| | a | |
2 paź 08:32
ania:
zadanie 3 to tylko 1 pitagoras ...obwód 32 wysokość 8
2 paź 08:34
ania:
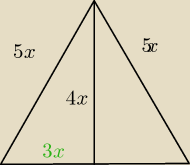
2 paź 08:36
wixik: ania:
ale właśnie z w odpowiedziach w książce jest inaczej w zadaniu 2
2 paź 12:16
Oj wixik:
uruchom myślenie
2 paź 12:30
pigor: .... tam w zad 2) jest dobrze − choć można było to zrobić ...

zgrabniej − tylko przekształć
wzór końcowy np. rozszerzając (mnożąc) jego licznik i mianownik przez "a", mianowicie:
| | b | | b*a | | ab | |
c= |
| = |
| = |
| − szukana długość boku c . |
| | | | | | a+b | |
2 paź 12:40
wixik: a fakt mój błąd
2 paź 17:36
wixik: wielkie dzięki
2 paź 17:42

 ha * a = hb * b = hc *c
ha * a = hb * b
ha * a = hb * b = hc *c
ha * a = hb * b

 zgrabniej − tylko przekształć
wzór końcowy np. rozszerzając (mnożąc) jego licznik i mianownik przez "a", mianowicie:
zgrabniej − tylko przekształć
wzór końcowy np. rozszerzając (mnożąc) jego licznik i mianownik przez "a", mianowicie: