zbiory
Joanna: |y|≤|x−1|
zaznacz w układzie współrzędnych zbiór rozwiązań nierówności
1 paź 20:01
mala: rozpatrz taki przypadek że |y| to f(x) a |x−1|= g(x)rozwiazaniem bd czesc wspolna, wartość f(x)
to wszystko nad osią x, bo y muszą byc dodatnie (najlepiej narysuj sobie wykres i zamaluj), a
|x−1| będzie
x ∊ <−1;1>
1 paź 20:17
mala: przepraszam źle wpisałem x∊(−∞;−1) i (1:∞)
1 paź 20:22
PuRXUTM:
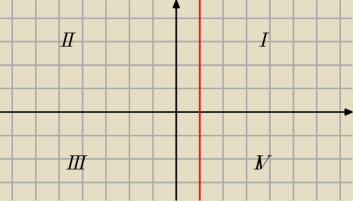
ja bym to zrobił tak, ale nie wiem czy dobrze
masz wartość bezwzględną więc patrzysz dla jakich wartości y czy x te wyrażenia pod wartością
bezwzględną się zerują
pierwsza się zeruje dla y=0 druga dla x=1 więc to są nasze jakby graniczne punkty więc rysujemy
sobie jakie mamy warunki dla poszczególnych wartości x ,y
teraz zapisujesz warunki
I dla y≥0 ⋀ x≥1 ( twoje równanie ma postać)
y≤x−1 ( podstawiamy sobie liczby z tego przedziału i sprawdzamy czy wartość wyjdzie ujemna czy
nie − mam nadzieje że wiesz o co chodzi

)
II dla y≥0 ⋀ x<1
y≤−x+1
i tak dalej jeszcze rozpisujesz dla III i IV
Później rysujesz wykres zaraz ci narysuje dla jednej ćwiartki żebyś wiedziała jak to robić
1 paź 20:26
Eta:
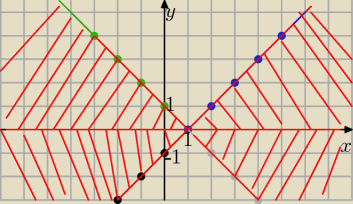
1 paź 20:30
PuRXUTM:
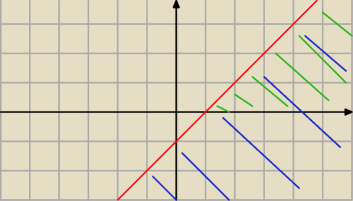
dla pierwszego przypadku wyszedł nam wzór y≤x−1
rysujemy sobie prostą y=x−1
zaznaczamy zgodnie z nierównością y≤x−1 ( kolor niebieski )
teraz patrzymy na dziedzinę mamy w założeniach do pierwszego przypadku y≥0 ⋀x≥1
więc patrzymy na nasz wykres i zaznaczamy to co mieści się w dziedzinie ( kolor zielony )
i to jest rozwiązanie dla pierwszego przypadku ( czyli tylko to na zielono )
z pozostałymi przypadkami robisz to samo i później wszystkie rozwiązania nanosisz na jeden
rysunek
1 paź 20:33
PuRXUTM: no nanosisz na jeden rysunek jak Eta

1 paź 20:34
olga: oj pamietam pamietam ten materiał

no nie zazdtoszcze

1 paź 20:38
Joanna: Eta wykres jest prawidłowy ale jak to rozpisać ?
1 paź 22:15
Eta:
1/ niebieski i zielony dla y≥0
to y≤ |x−1| i zaznaczasz część płaszczyzny pod wykresem V ,tylko w I i II ćw wraz z
osią OX
2/ dla y<0
−y≤|x−1| ⇒ y ≥ − |x−1| −−− zaznaczasz część płaszczyzny nad tym wykresem ( ramionami w
dół
wykres czarno− szary) ale dla y <0
1 paź 22:25
pigor: ... ja bym to opisał analitycznie np. tak :
|y| ≤ |x−1| /
2 ⇔ y
2 ≤ (x−1)
2 ⇔ y
2−(x−1)
2 ≤ 0 ⇔ (y−x+1)(y+x−1) ≤ 0 ⇔
⇔ (y−x+1 ≤ 0 ∧ y+x−1 ≥ 0) ∨ (y−x+1 ≥ 0 ∧ y+x−1 ≤ 0) ⇔
⇔ (y ≤ x−1
∧ y ≥ −x+1)
∨ (y ≥ x−1
∧ y ≤ −x+1) i rysujesz sumę iloczynów
zbiorów punktów nad i pod odpowiednimi prostymi w nawiasach . ...

1 paź 22:34
Eta:
Na jedno wychodzi
pigor 
1 paź 22:36
Boniek: Wszystko ładnie pięknie,ale jak nierówności nie możesz podnieść do kwadratu
17 paź 15:41
Omikron: Możesz, jeżeli obie strony są nieujemne.
17 paź 15:46
 ja bym to zrobił tak, ale nie wiem czy dobrze
masz wartość bezwzględną więc patrzysz dla jakich wartości y czy x te wyrażenia pod wartością
bezwzględną się zerują
pierwsza się zeruje dla y=0 druga dla x=1 więc to są nasze jakby graniczne punkty więc rysujemy
sobie jakie mamy warunki dla poszczególnych wartości x ,y
teraz zapisujesz warunki
I dla y≥0 ⋀ x≥1 ( twoje równanie ma postać)
y≤x−1 ( podstawiamy sobie liczby z tego przedziału i sprawdzamy czy wartość wyjdzie ujemna czy
nie − mam nadzieje że wiesz o co chodzi
ja bym to zrobił tak, ale nie wiem czy dobrze
masz wartość bezwzględną więc patrzysz dla jakich wartości y czy x te wyrażenia pod wartością
bezwzględną się zerują
pierwsza się zeruje dla y=0 druga dla x=1 więc to są nasze jakby graniczne punkty więc rysujemy
sobie jakie mamy warunki dla poszczególnych wartości x ,y
teraz zapisujesz warunki
I dla y≥0 ⋀ x≥1 ( twoje równanie ma postać)
y≤x−1 ( podstawiamy sobie liczby z tego przedziału i sprawdzamy czy wartość wyjdzie ujemna czy
nie − mam nadzieje że wiesz o co chodzi  )
II dla y≥0 ⋀ x<1
y≤−x+1
i tak dalej jeszcze rozpisujesz dla III i IV
Później rysujesz wykres zaraz ci narysuje dla jednej ćwiartki żebyś wiedziała jak to robić
)
II dla y≥0 ⋀ x<1
y≤−x+1
i tak dalej jeszcze rozpisujesz dla III i IV
Później rysujesz wykres zaraz ci narysuje dla jednej ćwiartki żebyś wiedziała jak to robić

 dla pierwszego przypadku wyszedł nam wzór y≤x−1
rysujemy sobie prostą y=x−1
zaznaczamy zgodnie z nierównością y≤x−1 ( kolor niebieski )
teraz patrzymy na dziedzinę mamy w założeniach do pierwszego przypadku y≥0 ⋀x≥1
więc patrzymy na nasz wykres i zaznaczamy to co mieści się w dziedzinie ( kolor zielony )
i to jest rozwiązanie dla pierwszego przypadku ( czyli tylko to na zielono )
z pozostałymi przypadkami robisz to samo i później wszystkie rozwiązania nanosisz na jeden
rysunek
dla pierwszego przypadku wyszedł nam wzór y≤x−1
rysujemy sobie prostą y=x−1
zaznaczamy zgodnie z nierównością y≤x−1 ( kolor niebieski )
teraz patrzymy na dziedzinę mamy w założeniach do pierwszego przypadku y≥0 ⋀x≥1
więc patrzymy na nasz wykres i zaznaczamy to co mieści się w dziedzinie ( kolor zielony )
i to jest rozwiązanie dla pierwszego przypadku ( czyli tylko to na zielono )
z pozostałymi przypadkami robisz to samo i później wszystkie rozwiązania nanosisz na jeden
rysunek

 no nie zazdtoszcze
no nie zazdtoszcze 

