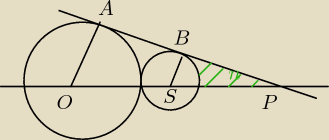
matura rosz. planimetria ak: okrąg o środku O i promieniu 3 jest styczny zewnętrznie do okręgu o środku S i promieniu 1. Prosta przechodząca przez środki tych okręgów przecina prostą styczną do obu okręgów w punkcie P. Oblicz miarę kąta BSP oraz pole zacieniowanego (na zieono) obszaru.o

albina: też się właśnie zastanawiam nad tym. pomoże ktoś?

irena_1: |OA|=3 |SB|=1 |OS|=4 |SP|=x

3		1
	=
4+x		x

3x=4+x 2x=4 x=2

	1
cosα=
	2

α=60⁰

	1
Od pola trójkąta trzeba odjąć		małego koła
	6

	1		1		π
P=		*1+2sin600−		π*12=√3−
	2		6		6

albina: dziękuję bardzo pod koniec znalazłam mały błąd ale i tak dziękuję

irena_1: No, tak, zaraz poprawię

	1		1		√3		1		3√3−π
P=		*1*2sin600−		π*12=		−		π=
	2		6		2		6		6

m: Czemu cosα=1/2?

cialo krzys: ale SP to x+1

wredulus_pospolitus: cialo −−− autor pierwszej odpowiedzi zaznaczył długość całego odcinka SP jako 'x', nikt mu nie broni przyjąć w taki sposób. możesz przyjąc |SP| = 1 + x ... ale to także zmieni proporcję (bo wtedy |OP| = 5+x