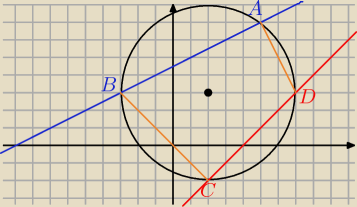
Czworokąt ABCD jest wpisany w okrąg ... Krystian: Tutaj mam prośbe o rozwiązanie tego trochętrudniejszego zadania: Czworokąt ABCD jest wpisany w okrąg (x−2)do potęgi +(y−3)do potęgi = 25. Bok AB zawiera się w prostej x−2y+9−0, zaś bok CD w prostej x−y−4=0. a) Oblicz współrzędne wierzchołków A,B,C,D. b) Oblicz równanie prostych AD i BC. c) Oblicz obwód czworokąta ABCD. d) Oblicz pole czworokąta ABCD. e) Oblicz współrzędne przecięcia przekątnych AC i BD.

Aga1.: Rozwiąż dwa układy równań równanie okrąg + równanie jednej prostej oraz okrąg+ druga prosta

asdf: (x − 2)² + (y − 3)² = 25 Prosta zawierająca punkty CD w okręgu: x − y − 4 ⇔ y = x − 4 (x − 2)² + (x − 4 − 3)² = 25 x² − 4x + 4 + x² − 14x + 49 = 25 2x² − 18x + 28 = 0 Δ = 324 − 224

	18 − 10
x1 =		= 2
	4

x₂ = 7 y₁ = x₁ − 4 ⇒ y₁ = −2 y₂ = x₂ − 4 ⇒ y₂ = 3 Współrzędnie punktów: C = (2; −2) D = (7; 3) Reszte podobnie