latwa caleczka? ania:

arctg√x
	bardzo prosze o pomoc w zrobieniu tej calki jak sie za to zabrac?
2√x(1+x)

Amaz: Podstawienie: t=√x.

ania: a moglby ktos machnac poczatek? (1 linijkę) dziekuje serdecznie♥

Amaz: Podstawienie: t = √x ⇒ t² = x dt = ^dx_2√x

ania: Dochodze do całki

arctg t
	dt ? czy aby napewno przez podstawienie?
1+t2

teraz powinnam rozbić tą calkie na dwie? AMAZ mogłbys jeszcze troche policzyc ta caleczke. Dzieki

ania: lub ktokolwiek inny

Amaz: Teraz następne podstawienie: s = arctg t ds = ^dt_1+t²

ania: Czy moge to tak "machnac"? u=arctg t v'=1

	1
u'=		v=t
	1+t2

...

	t
t arctg− Calka		(tutaj przez podstawienie A i B)
	1+t2

itd? ... sama calka

	t
Calka		<− prosta calka i na sam koniec podkladam za t?
	(t−1)(t+1)

Twoim sposobem

	1
Calka S ds =		s2+C
	2

a to daje

1
	(arctg√x)2+c − wynik?
2

troszke zmeczona jestem, takze przepraszam za ciezkie rozkminy...

Amaz: Wynik dobry. Tak na marginesie: (1+t²) ≠ (t+1)(t−1).

ania: hah, racja spie juz. Dzieki

ania: czy wynik z calki :

arcsin√x
	dx
√x(1−x)

to

	1
2[		(arcsin√x)2]+C
	2

prosze o sprawdzenie

pigor: ....ja bym robił np. tak:

	arcsin√x		dx
∫		dx= ∫ arcsin√x		=
	√x(1−x)		√x(1−x)

	dx
= | arcsin√x= t ⇒		= dt | = 2 ∫ tdt = 2*12t2+C=
	2√x*√1−x

= t²+C= (arcsin√x)² +C = arc²sin√x+C , a więc jest o.k. − mamy te same wyniki, choć nie ... takie same, ale po skróceniu u ciebie przez 2, będą już takie same . ...

ania: Oblicz pole obszaru ogarniczonego krzywymi: y=cos²x ; prosta y=1−x² oraz osią Ox jeszcze takie zadanko

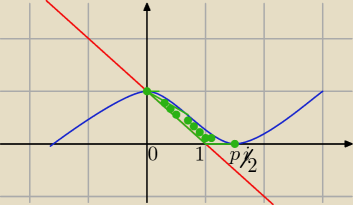
Basia: wykresem y = 1−x² jest parabola; popraw treść pewnie ma być: prosta y=1−x ₀∫¹ [ cos²x − (1−x) ]dx + ₁∫^π/2cos²xdx = ₀∫^π/2cos²xdx − ₀∫¹(1−x)dx

ania: http://pokazywarka.pl/4r0bhc/ Treść tego zadania jest na 100% poprawnie napisana,

ania: chociaz faktycznie pasowala by tam prosta, ale to zadanie musi byc poprawne (bylo na egzaminie dla 100osob~~). Dzieki za pomoc

ania: Oblicz pole obszaru ogarniczonego krzywymi: y=cos2x, y=1−x2 oraz osią Ox Czy nie trzeba czasami policzyc dwoch calek?

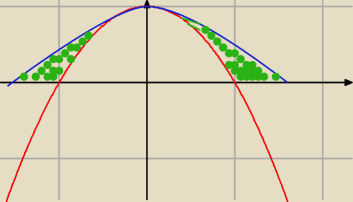
Basia: no to to jest banalnie proste te krzywe mają jeden jedyny punkt wspólny (0,1) zielone obszary są symetryczne względem OY czyli mają takie same pola P = 2*[₀∫^π/2cos²xdx − ₀∫¹(1−x²)dx]] albo bez wykorzystywania symetrii P = _−π/2∫^π/2cos²xdx − ₋₁∫¹(1−x²)dx