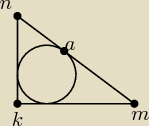 Witam prosze o pomoc
w trojkat prostokatny mnk wpisano okrag, punkt stycznosci A okregu do przeciwprostokatnej MN
podzielil te przeciwprostokatna na 2. odcinki uzasanij ze pole tego trojkata jest rowne |MA| x
|AN|
Witam prosze o pomoc
w trojkat prostokatny mnk wpisano okrag, punkt stycznosci A okregu do przeciwprostokatnej MN
podzielil te przeciwprostokatna na 2. odcinki uzasanij ze pole tego trojkata jest rowne |MA| x
|AN|
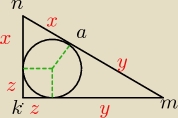 Oznaczmy przez x=|na| , y=|am , z=promień okręgu wpisanego
|nk|=x+z
|km|=y+z
|nm|=x+y
z tw. Pitagorasa:
(x+z)2+(y+z)2=(x+y)2
Po rozpisaniu i uproszczeniu dostajemy:
2z2+2xz+2yz=2xy / :2
z2+xz+yz=xy
Oznaczmy przez x=|na| , y=|am , z=promień okręgu wpisanego
|nk|=x+z
|km|=y+z
|nm|=x+y
z tw. Pitagorasa:
(x+z)2+(y+z)2=(x+y)2
Po rozpisaniu i uproszczeniu dostajemy:
2z2+2xz+2yz=2xy / :2
z2+xz+yz=xy
| 1 | 1 | 1 | 1 | |||||
PΔkmn= | *|km|*|kn|= | (x+z)(y+z)= | (z2+xz+yz+xy)= | (xy+xy)= | ||||
| 2 | 2 | 2 | 2 |
| 1 | ||
= | *2xy=x*y=|na|*|am| c.b.d.u | |
| 2 |
