oblicz miarę kąta dwuściennego w ostrosłupie
ania: oblicz miarę kąta dwuściennego przy podstawie ostrosłupa prawidłowego trójkątnego, jeśli
a) wysokość ostrosłupa jest trzy razy krótsza od wysokości podstawy
b) wysokość ostrosłupa jest dwa razy krótsza od krawędzi podstawy
Proszę o rozwiązanie z rysunkami, nie wiem gdzie zaznaczyć ten kąt i jak go obliczyć
29 wrz 18:13
dero2005:
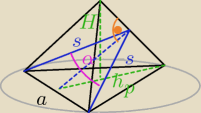
H − wysokość ostrosłupa
h
p − wysokość podstawy
α − kąt dwuścienny
29 wrz 19:47
dero2005:
H = 3h
p
23h
p = 2H
liczymy l (krawędź boczna)
l
2 = h
2 + (
23h
p)
2
l = H
√5
liczymy sinus kąta pochylenia krawędzi bocznej do podstawy
liczymy odcinek w (linia niebieska przerywana)
w = h
p*sinβ = H*
35√5
liczymy bok podstawy a
a =
23√3h
p = 2
√3H
liczymy odcinek s (linia niebieska ciągła)
s
2 = w
2 + (
a2)
2
liczymy ze wzoru cosinusów
a
2 = 2s
2 − 2s
2cosα
cos α = −
14
α = 104,47
o
trzeba sprawdzić prawidłowość wyliczeń
zad b podobnie tylko że, h
p = 2H
29 wrz 20:19
Mila: Dero, ten kąt ?
29 wrz 21:25
Mila:
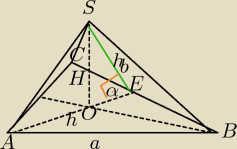
a)
α=45
0
b)
29 wrz 21:48
Mila: | | 1 | | 1 | | a√3 | | a√3 | |
|OE|= |
| h= |
| * |
| = |
| |
| | 3 | | 3 | | 2 | | 6 | |
| | 1 | | a√3 | | 1 | | 6 | |
tgα= |
| a:( |
| )= |
| a* |
| = |
| | 2 | | 6 | | 2 | | a√3 | |
α=60
29 wrz 21:51
ania: dziękuję Wam obojgu, choć odpowiedź Mili zgadza się z odp, a po drugie rozwiązanie jest
bardziej czytelne
Jedno pytanie− w tym przypadku kąt dwuścienny to kąt nachylenia ściany bocznej do podstawy?
29 wrz 22:08
Mila: Tak i cieszę się, ze odpowiedzi się zgadzają.

29 wrz 22:14
ania: jeszcze raz wielkie dzięki za pomoc

29 wrz 22:17
dero2005:
przyznaję sie bez tortury że pomyliłem kąty i policzyłem kąt dwuścienny ścian bocznych, moja
wina
29 wrz 23:04
ania: przynajmniej wiesz, że coś takiego istnieje i jak to się liczy

29 wrz 23:45
 H − wysokość ostrosłupa
hp − wysokość podstawy
α − kąt dwuścienny
H − wysokość ostrosłupa
hp − wysokość podstawy
α − kąt dwuścienny
 a)
a)


