pomoc Edzio: prosiłbym o pomoc. Narysuj wykres funkcji f(x)= 2|x² + x| − 4 nie mam pojęcia jak opuścić wartosć bezwzględna

SŁOŃCE POLSKIEJ MATEMATYKI: Sprawdz kiedy x²+x>0. To tak na dobry początek.

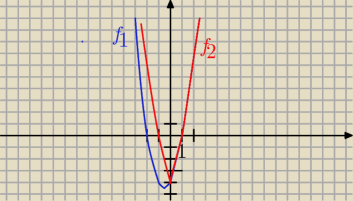
Beti: lub tak: 1^o rys. wykres funkcji y = 2x² + 2x − 4 −−> f₁ (obl. m. zer. i wierzchołek) 2^o zostawiasz tę część wykresu, która odpowiada x nieujemnym oraz jej symetryczne odbicie względem osi y −−> f₂

Basia: przecież to nieprawda Beti

Basia: x²+x≤0 ⇔ x(x+1)≤0 ⇔ x∊<−1;0> czyli mamy 2x²+2x−4 dla x∊(−∞;−1)∪(0;+∞) f(x) = −2x²−2x−4 dla x∊<−1;0>

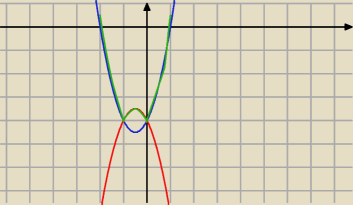
Basia: wykres to to zielone (trochę słabo widać)

pigor: ... no to może więcej ... światła i np. tak : f(x)=2|x²+x|−4= 2|x(x+1|−4= (2(x²+x)−4 ∧ x(x+1) ≥0) ∨ (2(−x²−x)−4 i x(x+1)<0) ⇒ { 2x²+2x−4 , gdy x≤ −1 ∨ x ≥0 ; f(x)= { ⇔ {−2x²−2x−4 , gdy −1< x <1 , { 2(x²+2x+1−5) , gdy x∊(−∞;−1> U <1;+∞) ⇒ f(x)= { ⇔ {−2(x²+2x+1+3) , gdy x∊(−1;1) , { 2(x+1)²−5 , gdy x∊(−∞;−1> U <1;+∞) ⇔ f(x)= { {−2(x+1)²+3 , gdy x∊(−1;1), ... i rysujesz części dwóch parabol : jedną o wierzchołku W=(−1,−5) i ramionach do góry w sumie przedziałów x∊(−∞;−1> U <1;+∞) i drugiej paraboli część o W=(−1,3) i ramionach do dołu w przedziale x∊(−1;1), także musisz jeszcze obliczyć punkty przecięcia się tych parabol (o ile istnieją) , no i ich miejsca zerowe byłyby istotne dla w miarę dokładnego narysowania tych parabol . ...

pigor: ... zobaczyłem wykresy Basia i widze swój błąd , bo nie wymnożyłem przez 2 , wtedy będą inne rzędne wierzchołków paraboli mianowicie −10 lub drugie 6 . ...

pigor: ... a może i coś więcej się znajdzie , ale znikam i nie będę szukał już.

Basia: przecież wymnożyłeś; błąd masz tutaj 2x²+2x−4 = 2(x²+2x+1−5) to raczej nie jest prawdą 2x²+2x−4 = 2(x²+x−2) = 2(x²+x+¹₄ − ¹₄−2) = 2[(x+¹₂)² − ⁹₄] = 2(x+¹₂)² − 4,5 W(−0,5; −4,5) w drugim jest ten sam błąd

pigor: ... racja, dzięki Basia ,

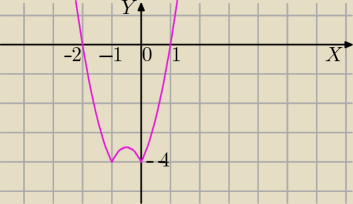
Mila: Wykres f(x), u Basi masz rozpisane.