losujemy dwie kule z urny, ile jest kul? Łukasz: Z urny, w której jest 1 kula czarna i pewna liczba kul białych, losujemy dwie kule bez zwracania. Ile jest kul białych, jeśli prawdopodobieństwo wylosowania dwóch kul białych jest równe 2/3? Proszę o pomoc w rozwiązaniu tego zadania i jeśli to możliwe to również o rozrysowanie go na drzewku.

Basia: 1 czarna + n białych czyli n+1 wszystkich n>1 bo dla n=1

	1		2
P(A) =		≠
	2		3

losujemy 2 kule

	n+1 2		(n+1)!		(n+1)!		n(n+1)
|Ω| =		=		=		=
			2!(n+1−2)!		2!(n−1)!		2

A − obie białe

	n 2		n!		(n−1)*n
|A| =		=		=
			2!(n−2)!		2

	|Ω|		n(n+1)		2		n+1
P(A) =		=		*		=
	|A|		2		n(n−1)		n−1

i rozwiązujesz równanie

n+1		2
	=
n−1		3

Basia: P.S. Drzewko zupełnie się do tego zadania nie nadaje

Basia: poprawka: n>1 bo dla n=1 mamy 1c i 1b czyli P(wylosowania dwóch b) = 0

Ajtek:

	|A|
Basia czy nie powinno być P(A)=
	|Ω|

Łukasz: Wielkie dzięki, a mogłabyś mi jeszcze wyjaśnić to: n>1 bo dla n=1 P(A)=1/2 ≠ 2/3?

Basia: oczywiście, że powinno; i będzie na odwrót; chyba jeszcze jedna kawa jest mi potrzebna, bo najwyraźniej śpię

Basia: ad.12:25 potem jest poprawka (12:22) myślałam o losowaniu jednej kuli, a przecież losujemy dwie dla n=1 masz 1c i 1b czyli nie da się wylosować dwóch białych czyli P(A)=0≠²₃ czyli warunki zadania nie są spełnione i oczywiście potem na odwrót

	|A|		n−1
P(A) =		= ..... =
	|Ω|		n+1

czyli

n−1		2
	=
n+1		3

Łukasz: Wszystko pięknie wyszło, dzięki

Buuu:

2		n		n−1
	=		*
3		n+1		n

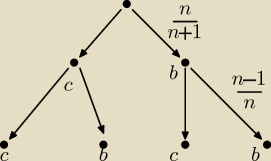
2		n2 − n
	=		; D: x∊R\{−1, 0}
3		n2 + n

3n² − 3n = 2n² + 2n n² − 5n = 0 n(n−5) = 0 n = 0 v n = 5 Co się Basiu drzewko nie nadaje

Basia: mnie się mam wrażenie, do niczego drzewko nie nadaje

Ajtek: Buuu z tą dzidziną to coś nie tak .