Zadania Godzio: Witam, Interesuje mnie zadanie 24, nie za bardzo wiem jak je rozgryźć, będę wdzięczny za pomoc

Trivial: A skąd?

Godzio: http://www.math.uni.wroc.pl/rekrutacja/files/test_2009_pyt.pdf Czasem nie myślę

konrad: jeżeli n jest liczbą parzystą to najdłuższe przekątne są takie same, jeżeli nieparzystą to najdłuższa przekątna jest krótsza od najdłuższej przekątnej dla n parzystego

konrad: tak mi się wydaję

Godzio: Trochę nie rozumiem Twojej wypowiedzi To, że dla n parzystego każdy wierzchołek ma swój "odpowiednik" po drugiej stronie to wiem, ale to dalej mi nic nie daje, wg Ciebie jakie by były odpowiedzi ?

konrad: a) nie b) tutaj oba n są nieparzyste i mam w związku tym wątpliwości, ale wydaje mi się, że dla n nieparzystych najdłuższa przekątna rośnie wraz z n, zatem 'tak' c) tak d) nie

konrad: ale ja tu specem nie jestem, więc są duże szanse że się mylę

Godzio: B,C − poprawne Czyli tak jak zaznaczyłeś, ale i tak średnio rozumiem dlaczego tak, a nie inaczej

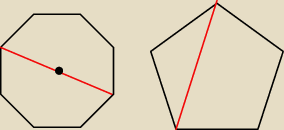
Trivial: Intuicyjnie: Dla n parzystego zawsze możemy wybrać wierzchołek odbity względem środka okręgu. Zatem P(n) = 2 dla n parzystego. Dla n nieparzystego nie możemy wybrać wierzchołka "przeciwległego", więc na pewno P(n) < 2 dla n nieparzystego. Dodatkowo, gdy n się zwiększa, nasza figura coraz bardziej przypomina okrąg, a zatem możemy wybierać coraz dłuższe połączenia. Zatem: P(n₁) < P(n₂) dla n₁ < n₂ oraz n₁ nieparzyste.

Trivial: I teraz rozwiązujemy. a) P(6)<P(8) b) P(5)<P(7) c) P(11)<P(14) d) P(10)<P(13) Zastępujemy to: a) 2<2 b) P(5)<P(7) c) P(11)<2 d) 2<P(13) Czyli mamy: a) false b) true c) true d) false

Godzio: Dzięki konrad i Trivial Jutro mam ten dziadowski test, mam nadzieję, że nie zrobię jakiś myłek i zdam go

TOmek: godzio to jutro razem z Toba bede nakur***** smoki na tescie. powodzenia xd

Godzio: I nawzajem Nie pasuje mi elementarna do mojego planu, więc nie ma opcji niezaliczenia

TOmek: tak po przemysleniu tego wszystkiego mysle ,ze mi przyda sie matematyka elemen. wiec za bardzo sie nie ucze.

Godzio: W sumie i tak mało przedmiotów jest więc nie ma problemu

konrad: o czyli jednak dobrze

Amaz: Godzio studiujesz na Uni Wro Matme?

Amaz: Aha bedziesz studiował Nie doczytałem

Godzio: Amaz już jestem oficjalnie studentem matematyki na UWr TOmek jak poszło ?

ICSP: Witaj Piotrusiu

Godzio: Witaj Mati

ICSP: ale my sobie słodzimy