geometria
hehe:
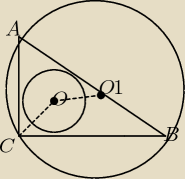
Czy ktoś mógłby mi wytłumaczyć, dlaczego odcinki AC i CO1 są równe, a nie AC i AO1 z
twierdzenia o odcinkach stycznych?
Treść zadania: W trójkąt prostokątny ABC, |∡ C | = 90, wpisano okrąg o środku w punkcie O oraz
opisano okrąg o środku O1 na tym trójkącie. Wyznacz |∡ B| i |∡A|, wiedząc, że :
a) |∡ OCO1| = 10
b) punkty O, O1, C są współliniowe.
28 wrz 18:30
Eta:
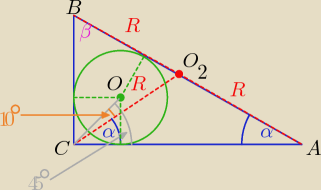
a)
CO zawiera się w dwusiecznej kąta prostego
ΔCAO
2 i ΔCBO
2 są równoramienne o boku "R"
α+β=90
o α= 45
o−10
o=.... to β=....
b) Jeżeli C, O, O
2 są współliniowe to trójkąt CAB jest prostokątny i równoramienny
zatem jakie są miary jego kątów ostrych?
28 wrz 19:25
Eta:
hehe ........ " przepisała i poszła ........ "

28 wrz 19:43
hehe: A dlaczego BC i BO2 nie mogą być równe z twierdzenia o odcinkach stycznych?
28 wrz 22:09
Eta:
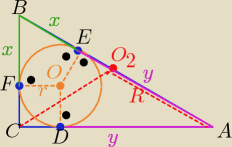
Czy teraz jasne?
28 wrz 22:38
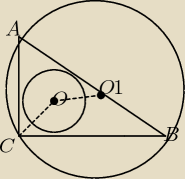 Czy ktoś mógłby mi wytłumaczyć, dlaczego odcinki AC i CO1 są równe, a nie AC i AO1 z
twierdzenia o odcinkach stycznych?
Treść zadania: W trójkąt prostokątny ABC, |∡ C | = 90, wpisano okrąg o środku w punkcie O oraz
opisano okrąg o środku O1 na tym trójkącie. Wyznacz |∡ B| i |∡A|, wiedząc, że :
a) |∡ OCO1| = 10
b) punkty O, O1, C są współliniowe.
Czy ktoś mógłby mi wytłumaczyć, dlaczego odcinki AC i CO1 są równe, a nie AC i AO1 z
twierdzenia o odcinkach stycznych?
Treść zadania: W trójkąt prostokątny ABC, |∡ C | = 90, wpisano okrąg o środku w punkcie O oraz
opisano okrąg o środku O1 na tym trójkącie. Wyznacz |∡ B| i |∡A|, wiedząc, że :
a) |∡ OCO1| = 10
b) punkty O, O1, C są współliniowe.
 a)
CO zawiera się w dwusiecznej kąta prostego
ΔCAO2 i ΔCBO2 są równoramienne o boku "R"
α+β=90o α= 45o−10o=.... to β=....
b) Jeżeli C, O, O2 są współliniowe to trójkąt CAB jest prostokątny i równoramienny
zatem jakie są miary jego kątów ostrych?
a)
CO zawiera się w dwusiecznej kąta prostego
ΔCAO2 i ΔCBO2 są równoramienne o boku "R"
α+β=90o α= 45o−10o=.... to β=....
b) Jeżeli C, O, O2 są współliniowe to trójkąt CAB jest prostokątny i równoramienny
zatem jakie są miary jego kątów ostrych?

 Czy teraz jasne?
Czy teraz jasne?