|x|<7 infii: |x|<7 jak rozwiązać takie równanie? Bedzie spojnik i więc trzeba wziąć czesc wspólną czyli rozwiazaniem bedzie zbiór pusty?

konrad: no część wspólną

joanna: nie bo przewracasz znak< w prawo i daje ∧ czyli i

Aga1.: IxI<7⇔−7<x<7⇔x∊(−7,7)

PW: Aga ma rację. Gdybyś był jednak bardzo dociekliwy i pytał, skąd się to wzięło, to z definicji wartości bezwzględnej: Jeżeli x < 0 to |x| = −x i nierówność przyjmuje postać x < 0 i −x < 7, czyli −7 < x <0. Jeżeli x≥0, to |x| = x i nierówność przyjmuje postać 0 ≤ x < 7 Zapisując łącznie obie możliwości (może mieć miejsce jedna l u b druga) mamy −7 < x <0 lub 0 ≤ x < 7 czyli w sumie (jest to suma przedziałów) −7 < x <7 jak napisała Aga. Warto to zapamiętać, żeby za każdym razem nie odkrywać na nowo.

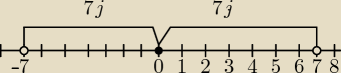
Mila: Do wyjaśnień Agi i PW dodam interpretację geometryczną. |x|<7 oznacza, że interesują nas liczby( na osi liczbowej) których odległość od 0 jest mniejsza niż 7 jednostek. x∊(−7;7)

Krzysiek : Przedzial jest jak najbardziej prawidlowo wyznaczony. jednak kolega Konrad ma racje ze jest to czesc wspolna (czyli iloczyn przedzialow ) a to dlatego ze IxI<7 zapiszemy tak x<7 czyli x∊(−∞,7) a takze zapiszemy ze x>−7 czyli x∊(−7 do ∞) . Teraz suma tych przedzialow to przedzial (−∞.∞) a nie przedzial (−7,7) ten ostatni przedzial to wlasnie czesc wspolna . Interpretacja geometryczna jak najbardziej prawidlowa

Krzysiek : Rozwiazanie tego zadania jest pokazane tam gdzie jest spis tresci. Jakby nasz sympatyczny kolega infii tam zobaczyl to mialby rozwiazanie podane na talerzu.

Basia: @PW Aga1 nie pisała o żadnej sumie przedziałów, bo to nie jest suma tylko iloczyn przedziałów: (−∞;7), który jest rozwiązaniem nierówności x<7 i (−7;+∞), który jest rozwiązaniem nierówności −7<x (czyli x>−7)

Aga1.: Można jeszcze tak IxI<7 x<7 i x>−7 Zaznaczyć rozwiązania nierówności na osi liczbowej i wyznaczyć część wspólną

PW: @Basiu, to j e s t s u m a, przecież zgodnie z definicją wartości bezwzględnej rozwiązujemy alternatywę układów nierówności: (x <0 i −x <7) l u b (x≥0 i x <7). Mila podała interpretację geometryczną − widać jak na dłoni, że jest to s u m a dwóch przedziałów, które są rozwiązaniami wyżej napisanych układów nierówności. Napisałem na końcu: Warto to zapamiętać, żeby za każdym razem nie odkrywać na nowo. Miało to taki sens, jak napisała Aga: |x| < 7 ⇔ −7 < x <7, ale oznacza to właśnie, że zamiast wynikającej z definicji wartości bezwzględnej alternatywy układów równań można rozwiązać układ równań. Jest to po prostu malutkie twierdzenie warte zapamiętania. To co pisze Krzysiek jest nie do zaakceptowania (cytuję): a to dlatego ze IxI<7 zapiszemy tak x<7 czyli x∊(−∞,7) a takze zapiszemy ze x>−7". To są "chwyty" zamiast stosowania definicji lub twierdzeń.

Basia: sto tysięcy razy (także w każdej szkole) udowodniono, że dla a≥0 |W(x)|<a ⇔ W(x)>−a i W(x)<a i wystarczy; po co to dowodzić po raz 100 001 ?

PW: Bo odpowiadałem na pytanie infii, który nie wiedział, jaki spójnik postawić, czyli zupełnie nie wiedział o co chodzi. Widocznie u niego w szkole tego twierdzenia nie było, albo przeoczył. Ponieważ jestem wrogiem rozwiązywania zada na zasadzie "jak to się robi", pokazałem dowód pisząc "gdybyś był jednak bardzo dociekliwy ...". Dojrzałem do tego, żeby przestać tracić czas tutaj, bo spotykam się nie po raz pierwszy z jakąś niezrozumiałą agresją, i to nie tych co pytali, ale tych, co podpowiadają, i to nie najlepiej. Pa.

Basia: Gdybyś czytał dokładnie zauważyłbyś, że infi wie, że ma być spójnik i. Bedzie spojnik i więc................ Sam to napisał. Nie wie chyba raczej jakie formy zdaniowe ten spójnik łączy. Dlatego Twój wykład wydał mi się niepotrzebny