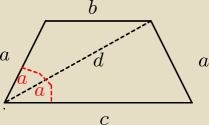
 Wykaż, że jeżeli przekątna trapezu równoramiennego zawiera się w dwusiecznej jego kąta ostrego,
to wtedy ramię trapezu jest równe krótszej podstawie.
Wykaż, że jeżeli przekątna trapezu równoramiennego zawiera się w dwusiecznej jego kąta ostrego,
to wtedy ramię trapezu jest równe krótszej podstawie.
| b | a | ||
= | |||
| sinα | sinα |
| b | ||
sin α ≠ | ||
| d |
| a | ||
sin α ≠ | ||
| d |
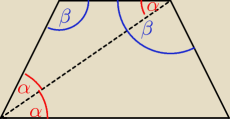 z warunków trapezu równoramiennego −> β + 2α = 180 ⇔ 2α = 180 − β
β + α + X = 180o (kąty wewnętrzne trójkąta ACD) ⇔ X = 180 − β − α = 2α−α = α
czyli ΔACD jest równoramienny, czyli a = b
z warunków trapezu równoramiennego −> β + 2α = 180 ⇔ 2α = 180 − β
β + α + X = 180o (kąty wewnętrzne trójkąta ACD) ⇔ X = 180 − β − α = 2α−α = α
czyli ΔACD jest równoramienny, czyli a = b
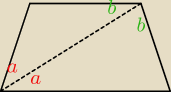 i jak jest dwusieczna, to ona dzieli na połowy tylko jeden kąt? czy jest tak jak na rysunku?
i jak jest dwusieczna, to ona dzieli na połowy tylko jeden kąt? czy jest tak jak na rysunku?

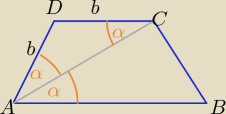 kąty BAC i ACD −−− naprzemianległe
ΔADC jest równoramienny o ramieniu długości "b" ⇒ |AD|= |D|C
kąty BAC i ACD −−− naprzemianległe
ΔADC jest równoramienny o ramieniu długości "b" ⇒ |AD|= |D|C
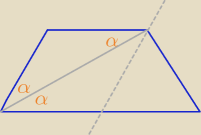

 , ale z tw. sinusów to jest zrobione źle? mój sposób w pierwszym poscie
, ale z tw. sinusów to jest zrobione źle? mój sposób w pierwszym poscie