W trójkąt wpisano koło, znajdź "l" (trudne zadanko) nakos: W trójkąt prostokątny wpisano koło. Znajdź najmniejszy możliwy obwód takiego trójkąta. Promień koła jest równe "r" Intuicyjnie wiem, że musi być to trójkąt równoramienny, ale nie potrafię tego udowodnić, poza tym w tym zadaniu należy liczyć pochodną, czy ktoś mógłby mi rozwiązać te zadanie? Bardzo proszę, męczę się z 3h i nic nie mogę wykombinować...

nakos: czy ktoś mi pomorze? dokładna treść zadania: Na kole o promieniu R opisano trójkąt prostokątny o najmniejszym polu. Znaleźć długości boków tego trójkąta. Będę dozgonnie wdzięczny za rozwiązanie

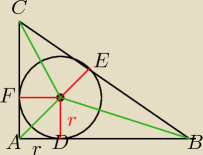
+-: Jest tu trochę zabawy AB=x; DB=BE=x−r; AC=y; CF=CE=y−r Pół obwodu p=x+y−r → y=p−x+r r=S/p; S=xy/2 → rp=xy/2 p=x+y−r ;2rp=x(p−x+r) p=(xr−x²)/(2r−x) p'=[(r−2x)(2r−x)+xr−x²]/(2r−x)²=(x²−4rx+2r²)/(2r−x)² 2r≠x Δ=... x1=r(2+√2) x2=r(2−√2) Oblicz p'' i określ max i min oblicz p=(xr−x²)/(2r−x) dla wyliczonego x oblicz y=p−x+r i okazuje się ono równe x zgodnie z przypuszczeniem

nakos: wielkie dzięki jesteś boski/a

nakos: wszystko do delty jest dla mnie zrozumiałe, a możesz mi jeszcze objaśnić takie kwestie: x>2r wiec x2 to jest sprzeczność zgadza się? a x1 jak to opisać zadaniowo, bo nie rozumiem tego wyniki? np. najmniejsza długości boku przy jakim da się narysować trójkąt na kole? czy co to jest? poza tym p" wychodzi mi (−4r²)/(2r−x)², dla dowolnego r wartość zawsze ujemna, więc funkcja jest wypukła ku górze, czyli jak policzyć min i max? punkt przegięcia 2r zgadza się, ale nie wiem co to daje? Na sam koniec mi wyszedł symbol nie oznaczony "y=y", więc już sam nie wiem gdzie robię błąd...

Basia: c = a−r+b−r c = a+b − 2r c² = a²+b² (a+b−2r)² = a²+b² a²+b²+4r²+2ab−4ar−4br = a²+b² 4r²+2ab−4ar−4br = 0 2r²+ab−2ar−2br = 0 b(a−2r) = 2ar−2r²

	2r(a−r)
b =
	a−2r

	2r(a−r)
c = a+		− 2r
	a−2r

	a(a−2r)+2r(a−r)−2r(a−2r)
c =
	a−2r

	a2−2ra+2ra−2r2−2ra+4r2		a2−2ra+2r2
c =		=
	a−2r		a−2r

	2ra−2r2		a2−2ra+2r2
L = a+		+
	a−2r		a−2r

	a2−2ra+2ra−2r2+a2−2ra+2r2
L =
	a−2r

	2a2−2ra
L =
	a−2r

	(4a−2r)(a−2r) − 1(2a2−2ra)
L' =		=
	(a−2r)2

4a2−8ra−2ra+4r2−2a2+2ra
	=
(a−2r)2

2a2−8ra+4r2
(a−2r)2

L'=0 ⇔ 2a²−8ra+4r²=0 ⇔ a² − 4ra + 2r² = 0 Δ = (−42)² − 4*1*2r² = 8r² √Δ = 2√2r

	4r−2√2r
a1 =		= 2r − √2r = (2−√2)r
	2

	4r+2√2r
a2 =		= 2r + √2r = (2+√2)r
	2

a∊(0; (2−2√2)r) ⇒ L'>0 ⇒ L ↗ a∊((2−√2)r; (2+√2)r) ⇒ L'<0 ⇒ L↘ a∊((2+√2)r;+∞) ⇒ L'>0 ⇒ L↗ czyli minimum masz dla a=(2+√2)r

	2((2+√2)r)2−2r((2+√2)r)
Lmin =		=
	(2+√2)r)−2r

2(4+4√2+2)r2 − 4r2 − 4√2r2
	=
√2r

12r2 + 8√2r2 − 4r2 − 4√2r2
	=
√2r

8r2 − 4√2r2
	=
√2r

4r2(2−√2)		4r(2−√2)
	=		=
√2r		√2

4√2(2−√2)r
	=
2

2√2(2−√2)r = (4√2 − 4)r = 4(√2−1)r mogłam się pomylić w rachunkach musisz to posprawdzać

+-: nakos powinno być (−4r²)/(2r−x)³, nie do 2 uBasiaj est błąd przy L powinno być wdrugim wierszu 2√2 a nie 4

Basia: wg.mnie (2+√2)² = 2² + 2*2*√2 + (√2)² = 4 + 4√2+2 = 6+4√2

+-: Basia mnie chodzi o Lmin 2 wiersz mianownik ostatni wyraz −2√2r² a nie 4√2r²

Basia: a tak teraz już widzę; no to rachunki "w końcówce" do poprawienia