funkcja adaś: Funkcja f każdej liczbie rzeczywistej x przyporządkowuje najmniejszą liczbę nieujemną a taką, że liczba x+a jest podzielna przez 4. Uzasadnij, że dla każdej liczby naturalnej n suma f(n)+f(n+1)+f(n+2)+f(n+3) ma stałą wartość. Nie wiem jak za to się zabrać, może zacznijmy od tego co to jest wartość stała

krystek: dla każdego x f(x)=b

adaś: dzięki , a można jeszcze jakoś inaczej zapisać, bardziej zrozumiale ?

Piotr: a wiesz jak wyglada wykres y=5 ? i ile wynosi wartosc funkcji np dla 2,4,5 itd ?

adaś: nie wiem co do mnie mówisz Piter

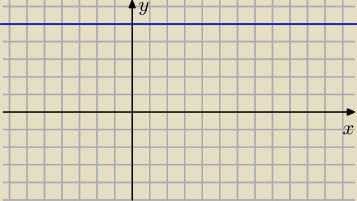
Piotr: to jest wykres funkcji y=5 to jest funkcja stala. dla kazdego x wartosc funkcji wynosi 5.

adaś: ok teraz widzę i rozumiem , ale wracając do zadania mamy dać takie liczby za n które po dodaniu dają liczbę podzielną przez 4 , takimi liczbami będą 0,1,2,3

krystek:

adaś: a że dodawanie jest przemienne to zmieniając kolejność tych liczb to i tak wyjdzie zawsze ta sama wartość, nie wiem czy dobrze kombinuje

krystek: @Piotr dlatego mój rys nie mógł się wgrać.

adaś: pomoże ktoś w tym zadaniu ?

Krzysiek : To z edodawanie jest przemienne to chwala CI za to ze wiesz. . Jednak w tym przypadku nie jest to CI potrzebne. Adas z tego co widze to TY masz problem ze zrozumieniem zadania . wroc sobie do wczorajszego postu z godziny 21:15. Ty musisz dac takie liczby a (czyli najmniejsza liczbe nieujemna) ktore po dodaniu do liczby n (naturalnej czyli 0,1,2 ,3, 4 ,5, 6, 7, 8, 9, itd az do∞)dadza liczbe podzielna przez 4 . Liczby podzielne przez 4 to 0, 4 ,8 ,12 16 20. 24, 28,32,36 itd co 4 . Zwroc naa to baczna uwage ze liczba 0 jest podzielna przez 4 . To teraz zabieramy sie do wykazania to co masz wykazac w zadaniu. Zauwaz ze teraz funkcja f ma teraz kazdej liczbie naturalnej n a nie kazdej liczbie rzeczywistej x ma przyporzadkowac najmiejsza liczbe nieujuemna taka ze teraz n +a ma byc podzielne przez 4 To do dziela . Najmniejsza liczba naturalna jest 0 wiec n=0 . jakie musi byc a zeby n+a bylo podzielne przez4 . nasze a =0 bo 0+0=0 i jest podzielne przez 4 Wobec tego f(0)=0 Teraz liczymy f(n+1) Nasz n =0 wiec n+1=1 mamy wiec f(1)= 3 bo bo musisz 3 dodac do 1 zeby dostac liczbe podzielna przez 4 , Teraz liczymy F(n+2) . Nasze n=0 wiec n+2 =2 ⇒f(2)=2 bo 2 musisz dodac do 2 zeby dostac liczbe podzielna przez 4 . Teraz f(n+3) . Nasze n=0 wiec n+3 =3 ⇒to f(3)=1 bo do 3 musisz dodac 1 zeby dostac liczbe podzielna przez 4 czyli 4 . Wobec tego suma f(0)+f(1)+f(2)+f(3)= 0+3+2+1=6 . Wezmy teraz np n=34 Ile teraz musisz dodac do 34 zeby otrzymac liczbe podzielna przez 4 i jak to bedzie liczba . Musisz dodac 2 zeby otrzymac liczbe 36 bo ona jest podzielna przez 4 . czyli f(34)=2 . n+1 to jest 35 ⇒f(35)=1 bo 35+1 =36 a to jest podzielne przez 4 , n+2 =36 ⇒f(36)=0 bo 36+0=36 a 36 jest podzielne przez 4 , n+3 =37 ⇒f(37) =3 bo 37+3=40 a 40 jest podzielne przez 4 . Zbierzmy to teraz do kupy i policzmy f(34)+f(35)+f(36)+f(37)= 2+1+0+3=6 . WYszla taka sama suma . Wez sobie jeszcze kilka takich liczb np n=100, . Wez sobie jesze kilka liczb np n=134 , n= 1342,n=280. Jesli dla f(134)+f(135)+f(136)+f(137) wyjdzie ci suma 6 i tak dla nastepnych to mozesz napisac dla kazdej liczby naturalnej n suma f(n)+f(n+1)+f(n+2)+f(n+3) ma stala wartosc. Oczywiscie dla tego zadania . Czesc.

adaś: dziękuje serdecznie ! ,teraz zaczynam rozumieć, lecz czy wystarczy tylko przedstawić kilkanaście liczb wyliczyć sumę i pokazać że ta suma jest stała dla tych kilkunastu liczb ?

Basia: nie wystarczy; masz udowodnić, że dla każdego n f(n)+f(n+1)+f(n+2)+f(n+3) = C liczby n, n+1, n+2 i n+3 to cztery kolejne liczby naruralne musi więc być tak, że jedna przy dzieleniu przez 4 daje resztę 0, druga 1, trzecia 2, a czwarta 3 czyli do jednej musisz dodać 0, do drugiej 3; do trzeciej 2 a do czwartej 1 czyli f(n)+f(n+1)+f(n+2)+f(n+3) = 0+3+2+1 = 6