Geometria Analityczna, Przestrzenna 3 zdanka z liceum matma rozsz. wytrwaly: 1. Dany jest okrąg o₁:x²+y²+6x+5=0 i okrąg o₂:x²+y²−12x+8x+27=0 Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu o₁ jest okrąg o₂. 2. Rozwiąż trójkąt mając dane R=15, a=15, b=15{3} 3. W trójkącie dane są trzy boki a=3 b=4 c=6. Oblicz cosinusy kątów tego trójkąta 3 Zadanka z którymi miałem problem ucząc się do sprawdzianu. Nie było mnie na jednokładności i mam lekkie problemu z zdankami tego typu, proszę pomoc najlepiej z wytłumaczeniem toku myślenia nad zadaniami.

PW: 1. Zapisać równania tak, żeby było widać środki i promienie okręgów (dopóki tego nie zrobisz, to nawet nie wiesz, czy to są okręgi, a przecież bywają zadania, w których bada się umiejętność analizowania danych). Mając środki S₁ i S₂ oraz promienie r₁ i r₂ trzeba wziąć jednokładność o skali

	r2		r2
		lub −		,
	r1		r1

a środek wymyślić gdzieś na prostej S₁S₂ w zależności od wzajemnego położenia okręgów. Po zrobieniu rysunku powinno się samo narzucić, gdzie to jest (podpowiedź: S₁ musi się przekształcić na S₂.).

wytrwaly: rozumiem zaraz to sobie rozpisze

Mila: Zadanie 1) http://www.zadania.info/d36/1/200 Jest wytłumaczone z ilustracją. Przeczytaj i i wpisz ewentualne pytania. Zadanie2) a=15 b=15√3 R=15 Z tw sinusów

b
	=2R ⇔b=2R*sinβ
sinβ

15√3=2*15*sinβ

	√3
sinβ=
	2

β=60⁰ lub β=120

a
	=2R ⇔a=2R*sinα
sinα

15=2*15sinα

	1
sinα=
	2

α=30⁰ γ=180−(30+60)=90

	1
spr. czy R=		c
	2

c²=15²+(15√3)² c²=225+225*3 c²=225*(1+3)=225*4 c=15*2=30 zgodność rozważ II przypadek β (β>α)

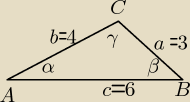
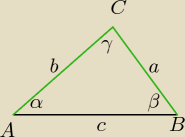
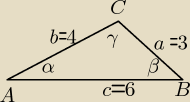Mila: W trójkącie dane są trzy boki a=3 b=4 c=6. Oblicz cosinusy kątów tego trójkąta. Z twierdzenia cosinusów: c²=a²+b²−2bccosγ 6²=3²+4²−2*3*4*cosγ 36=9+16−24cosγ 36−25=−24cosγ dokończ