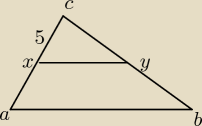
Wymiekam Szlag: Planimetria w trojkacie ABC : XY||AB. Pole trojkata XYC jest rowne 4cm2 , a pole trapezu wynosi 12cm2.wyznacz dlugosc odcinka AX, wiedzac ze CX wynosi 5 cm. Doszedlem do tego ze trojkat ABC ma 16 cm 2 i podobienstwo wynoci 4 tylko niewiem ajk to wykorzystac. prosze o jakas podpowiedz

Janek: ABC = 16 cm 2 CXY = 4 cm 2 k = 4 wiec CX = 5 a Xa = 20 bo 5 * 4 tyle daje

Szlag : nie moze wyjsc 20 wtedy ten trojkat bylby chyba o wiele za duzy w odpowiedziach pisze 10 czyli tak jakby CA = CX =5 i Xa =5 tylko jak to rozpisac zeby tyle wyszlo

Szlag : nie moze wyjsc 20 wtedy ten trojkat bylby chyba o wiele za duzy w odpowiedziach pisze 10 czyli tak jakby CA = CX =5 i Xa =5 tylko jak to rozpisac zeby tyle wyszlo

Szlag: pomoze ktos chociaz troche

ICSP: Napiszę Ci to tylko daj mi chwilkę.

ICSP: Z danych mam : P_ΔXYC = 4cm² P_{trapezu ABXY} = 12cm² zatem P_ΔABC = 12cm² + 4cm² = 16cm² ale wiemy że : Δ_XYC ≈ Δ_ABC z cechy kkk (rozpisz dokładniej dlaczego są podobne) zatem :

CX
	= k
AC

ale wiemy przecież że :

PΔXYC		4		1
	= k2 ⇒		= k2 ⇒ k =		(skala podobieństwa jest zawsze
PΔABC		16		2

dodatnia) zatem :

1		5
	=		⇒ AX = 5
2		5+AX

Szlag: bardzo dziekuje za to odpowiedz

pigor: ... , otóż, jak na mój ... gust z warunków zadania i tw. o stosunku figur podobnych, jeśli k − skala podobieństwa, to

4		4		1
	=		=		=(12)2= k2 ⇒k=12, zatem z własności podobieństwa
12+4		16		4

|cx|		5		1
	= k ⇔		=		⇔ |ax|+5= 10 ⇔|ax|= 5, a więc na pewno
|ca|		|ax|+5		2

w odpowiedzi jest długość |ax| , bo może jest to |ac|= 5+5= 10 . ...