Funkcja wykładnicza Ania: Mam do rozwiązania taką nierówność: 2^2x+10^x>6^x+15^x Ogólnie nie skomplikowany przykład, ale dochodzę do wyniku; 2^x=3^x ⋁ 2^x=−5x raczej się nie pomyliłam Nie mam pojęcia co można z tym dalej zrobić(dodam że mogą tu pomóc logarytmy, ale jednak szukam innego rozwiązania, gdyż logarytmów jeszcze nie miałam i ich nie umiem)

Bogdan: To jest nierówność: 2^2x + 2^x*5^x − 2^x*3^x − 3^x*5^x > 0 ⇒ (2^2x − 2^x*3^x) + (2^x*5^x − 3^x*5^x) > 0 2^x(2^x − 3^x) + 5^x(2^x − 3^x) > 0 ⇒ (2^x − 3^x)(2^x + 5^x) > 0 W otrzymanym iloczynie: 2^x + 5^x > 0 dla dowolnych wartości x. Skoro iloczyn jest dodatni, to dodatnie jest także wyrażenie 2^x − 3^x. Trzeba teraz rozwiązać nierówność: 2^x − 3^x > 0

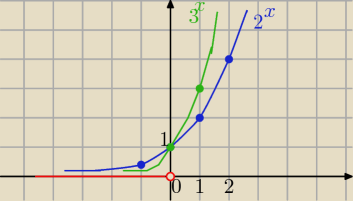
Eta: Po przekształceniach otrzymasz: (2^x+5^x)(2^x−3^x) >0 , ponieważ 2^x3^x >0 dla x€R to pozostaje rozwiązać nierówność 2^x−3^x>0 ⇒ 2^x>3^x ⇔ x€ (−∞, 0) ( zobacz też na wykresie

Eta: poprawiam zapis : ponieważ 2^x+3^x >0 dla x€R

Eta: Witam Bogdanie Rysowałam i nie widziałam Twojego wpisu Miłego dnia

Bogdan: Witam Eto, pozdrawiam

Ania: Dzięki wielkie teraz jeszcze tylko to ogarnę