 r=23h
r=23h
| a√3 | ||
h= | ||
| 2 |
| 2 | 3 | |||
r= | h →h= | r | ||
| 3 | 2 |
| a√3 | ||
h= | ||
| 2 |
| 3 | a√3 | ||
r= | /2 | ||
| 2 | 2 |
| 3r | |
=a | |
| √3 |
| 3√3r | |
=a | |
| 3 |
| 1 | ||
R = | a√3 /*√3 ⇒ a = R√3 | |
| 3 |
 Dziękuję za odpowiedzi. Chciałbym jednak aby tę zależność wykazać a nie korzystać ze wzorów.
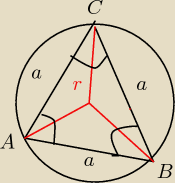
Jako, że to trójkąt równoboczny − kąty CAB, ABC, ACB są równe i mają miarę 60 st. Kąty BAr ma
miarę 30 st. a kąt ASB ma miarę 120 st (kąt środkowy oparty na tym samym łuku co kąty mające
60 st i oparte na okręgu).
jak korzystając pociągnąć dalej to rozumowanie aby dojść do tego, że a = R√3?
Dziękuję za odpowiedzi. Chciałbym jednak aby tę zależność wykazać a nie korzystać ze wzorów.
Jako, że to trójkąt równoboczny − kąty CAB, ABC, ACB są równe i mają miarę 60 st. Kąty BAr ma
miarę 30 st. a kąt ASB ma miarę 120 st (kąt środkowy oparty na tym samym łuku co kąty mające
60 st i oparte na okręgu).
jak korzystając pociągnąć dalej to rozumowanie aby dojść do tego, że a = R√3?
 Np. tak:
Środek okręgu opisanego to punkt przecięcia symetralnych boków.
Np. tak:
Środek okręgu opisanego to punkt przecięcia symetralnych boków.
|
| √3 | |||||||||||||||||||
W trójkącie prostokątnym ADS: | = cos30o ⇒ | = | |||||||||||||||||||
| R | R | 2 |
| a | ||
= 2R. | ||
| sinα |
| √3 | ||
Jak wiadomo w trójkącie równobocznym α = 60°, a sin60° = | , | |
| 2 |
| a | ||||||||
= 2R, | ||||||||
|
 Rozwiązanie PW też, pod warunkiem, że (jak sam napisał) mrrr zna już twierdzenie
sinusów.
Rozwiązanie Anny jest może nieco dłuższe, ale nie wymaga pamiętania żadnych wzorów
(bo i wysokość można sobie policzyć z tw.Pitagorasa) i nie wymaga znajomości funkcji
trygonometrycznych, a jedynie znajomości cech trójkąta równobocznego.
Może je więc również wykorzystać gimnazjalista.
Rozwiązanie PW też, pod warunkiem, że (jak sam napisał) mrrr zna już twierdzenie
sinusów.
Rozwiązanie Anny jest może nieco dłuższe, ale nie wymaga pamiętania żadnych wzorów
(bo i wysokość można sobie policzyć z tw.Pitagorasa) i nie wymaga znajomości funkcji
trygonometrycznych, a jedynie znajomości cech trójkąta równobocznego.
Może je więc również wykorzystać gimnazjalista. 