Zadanie z fizyki DOBRYMATEUSZ: 1. Paralaksa geocentryczna satelity wynosi 30 stopni. Na jakiej wysokości nad Ziemią się on znajduje? 2. Wyznacz graficznie paralaksę geocentryczną Księżyca. Wykonaj rysunek w odpowiedniej skali.

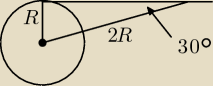
MQ: 30R22R

DOBRYMATEUSZ: Nie mam pojęcia jak to dokończyć

MQ: Nie ma czego dokańczać. Rysunek wynika z właściwości trójkąta prostokątnego, którego jeden z kątów ostrych ma 30^o R −− promień Ziemi 2R −− odległość od środka Ziemi do satelity.

DOBRYMATEUSZ: czyli odległość satelity to po prostu średnica Ziemi, tak?

MQ: Na to wychodzi

DOBRYMATEUSZ: ale odległością jest przyprostokątna, czy przeciwprostokątna 2R?

MQ: Sorry, przeczytałem jeszcze raz pytanie: Pytanie jest o wysokość nad Ziemią, więc 2R (odległość od środka Ziemi) minus R (promień Ziemi Wychodzi więc 2R−R=R CZyli nad Ziemią w odlełości równej promieniowi Ziemi. PS. Odc. o dł. 2R jest oczywiście przeciwprostokątną.

DOBRYMATEUSZ: w odpowiedziach mam że znajduje się na wysokości 4700 km

MQ: Nie wiem, skąd im tyle wyszło. Opis metody masz np. tu: http://draco.uni.opole.pl/moja_fizyka/numer6/artykuly/prezentacjan.html Nawet jeśli przyjmiemy, że trójkąt OKL jest równoramienny, to nie wychodzi 4700km, tylko więcej.

DOBRYMATEUSZ: a w tym 2 zadaniu że 1 stopień

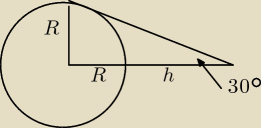
MQ: Już wiem jak to liczyli!

R
	=tg30o
R+h

Stąd

	R
h=		−R
	tg30o

I wychodzi tyle, ile trzeba, ok. 4700km

MQ: Ad 2. Dokładnie 57' czyli prawie 1^o

Dominika: PROSZĘ O POMOC, KOMPLETNIE TEGO NIE UMIEM! 1. Odległość do gwiazdy od Ziemi wynosi 40 AU. Ile wynosi jej paralaksa heliocentryczna? 2. Odległość do obiektu od Ziemi wynosi 163, 1 l .y. Ile wynosi jej paralaksa geocentryczna? 3. Jaka jest prędkość liniowa punktu obracającego się wokół środka w odległości 1,50 mm, jeżeli obraca się z częstotliwością 1200000r/min?