prawdopodobieństwa orety: wiedząc, że P(A')=1/2, P(A∪B)= 7/10 P(A∩B)=3/8 Oblicz P(B/A) wiem, że należy skorzystać ze wzoru P(A∪B)=P(A)+P(B)−P(A∩B) ale nie wiem jak

Eta:

	1
P(A)= 1−P(A')=
	2

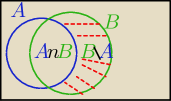
ze wzoru P(AUB)= P(A)+P(B) −P(A∩B) to: P(B)= P(AUB)_P(A)+P(A∩B) B\ A= B \ (A∩B) to: P(B)= P(B)− P(A∩B)=.........

Eta: Poprawiam zapis: P(B)= P(AUB) − P(A)+P(A∩B) =.........

Eta: @orety ....... zaniemówiłaś?

orety: staram sie rozwiazac nastepne idac tym tropem ale dzięki bardzo

Eta:

Gustlik:

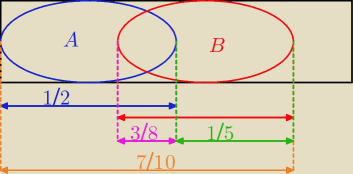
	1		7		3
wiedząc, że P(A')=		, P(A∪B)=		P(A∩B)=		Oblicz P(B/A)
	2		10		8

	1		1		1
P(A')=		⇒ P(A)=1−		=
	2		2		2

Wystarczy dobrze rozrysować, nanieść prawdopodobieństwa jako "rozmiary" zbiorów i niepotrzebne są wzory:

	7		1		7		5		2		1
P(B\A)=		−		=		−		=		=
	10		2		10		10		10		5