prawda?
adaś:
Mam polecenie ↓
Wyznacz największą wartość funkcji
ale ja zauważam że największa wartość nie istnieje mam rację ? Ponieważ współczynniki
kierunkowy
jest dodatni , czyli parabola w górę, jak w górę to wartości jest nieskończenie wiele.
26 wrz 19:17
asdf: to chyba nie jest parabola
26 wrz 19:19
Artur_z_miasta_Neptuna:
| | stała > 0 | |
fukcja postaci: f(x) = |
| będzie miała NAJWIĘKSZĄ WARTOŚĆ dla punktu, dla |
| | g(x) | |
którego g(x) przyjmuje wartość NAJMNIEJSZĄ.
Czyli musisz wyznaczyć wierzchołek g(x)
26 wrz 19:19
Artur_z_miasta_Neptuna:
tfu tfu tfu ...oczywiście f(x) największe dla g(x) najbliżej zeru (ale większe niż zero) ... co
de facto sprowadza się do dalszego rozumowania −−− wyznaczyć wierzchołek paraboli 2x2 − x + 1
26 wrz 19:21
26 wrz 19:25
adaś: | | 1 | | 7 | |
oczywiście dane xw= |
| i yw= |
| odnoszą się do mojego zadania na samej górze |
| | 4 | | 8 | |
26 wrz 19:26
Artur_z_miasta_Neptuna:
przeczytaj co napisałem i już masz gotowe rozwiązanie
26 wrz 19:27
asdf:
 y = 2x2 − x + 1
y = 2x2 − x + 1
2x
2 − x + 1:
Δ = −7
26 wrz 19:28
Artur_z_miasta_Neptuna:
a największa wartość funkcji to:
26 wrz 19:31
adaś:
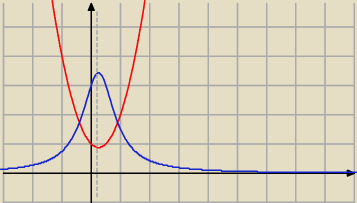
dlaczego dwa wykresy , jak rozumieć tą niebieską linię?
26 wrz 19:33
Artur_z_miasta_Neptuna:
niebieska linia to wykres f(x)
a czerwona to wykres SAMEGO mianownika
26 wrz 19:36
adaś:
nie może to być tylko czerwony wykres? Najpierw obliczam deltę potem wierzchołki i rysuje
wykres, zapomniał bym rysować jakiś wykres niebieski . Wtedy największa wartość by nie
istaniała
26 wrz 19:41
asdf: Jejciu, po prostu wyjaśniłem Ci to w sposób graficzny co napisał Artur.
26 wrz 19:44
adaś:
Nie rozumiem dwa wierzchołki jeden niebieski drugi czerwony i który brać pod uwagą , nawet jak
bym brał pod uwagę czerwony to nie wiem skąd te dwie funkcje , wierzchołki są na lini
niebieskiej i czerwonej , dlaczego czerwoną bierzemy pod uwagę? Najpierw funkcja idzie do góry
potem się zaniża , nie rozumiem
26 wrz 19:51
asdf: | | 3 | | 3 | |
To może inaczej, co jest większe? |
| , czy |
| |
| | 1 | | 7 | |
26 wrz 19:55
26 wrz 19:56
asdf: No to liczysz punkt, w których parabola "jest najniżej", a później masz:
h(x) = 2x
2 − x + 1
a > 0! ramiona w górę − to też trzeba wziąć pod uwagę!
| | 3 | | 3 | |
maksymalna wartość równania f(x) = |
| to y = |
| |
| | h(x) | | q dla h(x) | |
26 wrz 20:03
asdf: Przeczytaj kilka razy post Artura, a na pewno zrozumiesz!
26 wrz 20:04
klaudia: pomocy pomoże mi ktoś
26 wrz 20:04
klaudia: ciągi arytmetyczne
26 wrz 20:10
26 wrz 20:12
adaś: ?
26 wrz 20:12
adaś: zadania Klaudia na forum zadankowym "Dodaj nowe zadanie"
26 wrz 20:13
asdf: a > 0, zwf <q; ∞), inaczej, najwieksza wartosc nie istnieje...Probuj to zrozumiec...
26 wrz 20:14
adaś:
czy to funkcja będzie miała najmniejszą wartość?
26 wrz 20:19
adaś: chodzi mi o moje zadanie na samej górze , czy będzie miała niajmniejszą wartość?
26 wrz 20:30
adaś: Odpowie ktoś na ostatnie moje pytanie?

26 wrz 20:52
adaś: czy tutaj najmniejsza wartość będzie istniała?
29 wrz 16:05
Basia: odpowiedź masz na tym rysunku (26 września 19:28)
niebieska linia to wykres Twojej funkcji
29 wrz 16:07
adaś: | | 7 | |
wartość najmniejsza to |
| ? |
| | 8 | |
29 wrz 16:09
Basia:
nie; ta funkcja nie ma wartości najmniejszej
jej wartości dążą do 0, ale tego zera nie osiągają
29 wrz 16:12
Aga1.: adaś miałeś podać największą wartość funkcji.
29 wrz 16:16
adaś: a kiedy funkcja przyjmuje wartości najmniejsze?
29 wrz 16:18
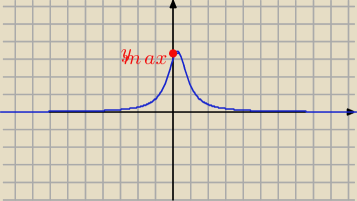
Aga1.:
29 wrz 16:20
adaś: a ta czerwona linia to co to jest ? Bo jak rysuje wykres to wychodzi mi ta czerwona funkcja a
nie ta niebieska
29 wrz 16:22
Aga1.: Ta funkcja nie przyjmuje wartości najmniejszej, bo
jej zbiór wartości to (0,ymax>
29 wrz 16:22
Basia: ta czerwona linia to wykres mianownika
29 wrz 16:23
Aga1.: Czerwona to sam mianownik, a niebieskiej to łatwo nie narysujesz (bez komputera).
29 wrz 16:24
adaś: bo to jest zadanie z podstawy , a mi się wydaje że dla maturzysty to nie jest taki proste aby
zrozumieć z wiadomości z liceum
29 wrz 16:26
adaś: skoro jej nie narysuje , to jak rozpoznać kiedy ma wartość najmniejszą a kiedy największa?
29 wrz 16:27
adaś: ?
29 wrz 16:44
Basia:
Ułamek, którego licznik jest liczbą stałą przyjmuje:
(a) wartość największą ⇔ jego mianownik przyjmuje wartość najmniejszą
(b) wartość najmniejszą ⇔ jego mianownik przyjmuje wartość największą
29 wrz 16:48
Basia:
ma być:
Ułamek, którego licznik jest liczbą stałą dodatnią przyjmuje:
29 wrz 16:49
Aga1.: Nie wydaje mi się by to zadanie było z podstawy.
Jeśli tak, to przeczytaj uważnie post Artura z 26 wrz. 19:19 i tego się trzymaj (bo przybliżony
wykres narysujesz jak będziesz miał dużo, dużo więcej wiadomości wykraczających poza program
LO)
29 wrz 16:50
adaś:
Było na arkuszu podstawowym, ja się dziwie takie zadania dawają z zakresu rozszerzonego czy
nawet poza materiałem z lo, a używać metod z zakresu np. rozszerzonego na maturze podstawowej
zabraniają .
29 wrz 16:58
adaś: przyjmuje wartość największą tam gdzie mianownik przyjmuje najmniejszą ,sądzę że tych info będę
się trzymał,dziękuje
29 wrz 17:01



