Suma kwadratów sinusów mirek: Wykaż, żę w tójkącie prostokątnym suma kwadratów sinusów jego katów jest równa jeden. −−−−−−− czyli tak ? sin^α+sin²β=1 I co dalej? może ktoś pomóc?

kamil: pomagam

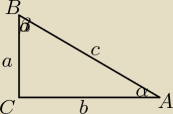
kamil: a teraz przy pomocy rysunku(zaleznosc miedzy bokami) zapisz sinα i sinβ. mam nadzieje ze wysatarczajaco Cie naprowadzilem. jesli bedziesz mial jeszcze problem daj znac

Squall: Dodam tylko, że tw. Pitagorasa się przyda

Bogdan: Zadanie jest sformułowane tak: Wykaż, że w trójkącie prostokątnym suma kwadratów sinusów jego katów jest równa jeden. Nie ma w zadaniu informacji, że chodzi o kąty ostre, a to oznacza, że trzeba uwzględnić wszystkie kąty trójkąta, również kąt prosty. W trójkącie prostokątnym suma kwadratów sinusów kątów nie jest równa1, jest równa 2. sin²90^o + sin²α + sin²(90^o − α) = 1 + sin²α + cos²α = 1 + 1 = 2. Gdyby treść zadania była taka: Wykaż, że w trójkącie prostokątnym suma kwadratów sinusów jego katów ostrych jest równa jeden, to rozwiązanie jest następujące: sin²α + sin²(90^o − α) = sin²α + cos²α = 1 Przypominam, że cos(90^o − α) = sinα oraz sin(90^o − α) = cosα

mirek: To zadanie musiało przesnać mojego nauczyciela, bo na krtce, którą mi dał zamazał 2 i zastąpił 1, bo pewnie myślał, ze błąd w druku. ;−) Dziekuję :0