Oblicz całkę potrójną czesław: ∫∫∫ v = (x²+y²) dxdydz gdzie V jest obszarem ograniczonym płaszczyznami x=0 y=0 z=0 z+z=a

Vizer: Popraw dane, bo raczej coś pomotałeś.

czesław: ∫∫∫_v reszta jest ok

Vizer: Czyli na końcu jest na 100% z + z = a ?

czesław: sorka x+z=a

Vizer: Granice całkowania : 0 < x < a 0 < y < a 0 < z < a − x Całka wygląda tak : ∫₀^a dx ∫₀^a dy ∫₀^{a − x} (x² + y²) dz

czesław: dzieki

Basia: x=0 ⇒ płaszczyzna YOZ y=0 ⇒ płaszczyzna XOZ z=0 ⇒ płaszczyzna XOY czy ja czegoś nie rozumiem, czy to jest jeden punkt ?

Vizer: Nie, to jest ograniczanie przez płaszczyzny, to tak jak czasem mamy np. ograniczone prostą y = x i y = x² i nie będzie to punkt, czyli część wspólna, tylko obszar pomiędzy tymi dwoma krzywymi.

czesław: wynik powinien wyjść tak jest w książce a⁵ /4

Vizer: No i co wychodzi? Bo nie liczyłem tej całki powiem szczerze.

czesław: No nie wiem coś mi się mota ..

Ania: oblicz macierz odwrotna 1 2 −1 0 4 −2 −3 0 2 1 −1 0 1 1 0 0 5 3 0 5 1 −1 4 1 1 −1 2 1 3 0 −2 0 1 2 1 5

Ania: pomyliłam sie i nie tu wstawiłam

Basia: @Vizer a co jest obszarem ograniczonym płaszczyznami XOY i XOZ i YOZ ?

Jack: Vizer, miałeś na myśli nierówności (zapewne) podczas, gdy tu stoją równości...

Vizer: Rozumuje to tak, że ten obszar ma się mieścić między tymi płaszczyznami, czyli dla "2d" gdy mamy między x = 0 i y = 0 to ma się na myśli ćwiartki układu współrzędnych, a która dokładnie to wyznaczana jest przez daną inną krzywą. Nie widzę tu błędu w treści. Ale muszę się przyznać, ze chyba się pospieszyłem ze swoim wynikiem (nie rysowałem, tylko wyobrażałem go sobie) i nie mogę znaleźć żadnego ograniczenia na y.

Ania: ∫₀ ^a dx ∫₀ ^a dy ∫₀ ^a−x (x² +y²)dz

Ania:

	a2 x2		a4 x		x4 a		x2 a3		a5
[		+		−		−		]0 a =
	3		3		4		6		4

Vizer: No właśnie Ania to jest chyba źle, bo skąd niby ograniczenie na y, że musi być mniejsze od a?

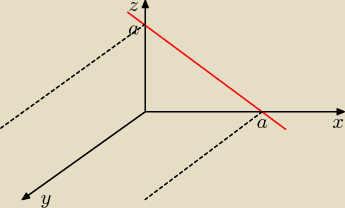
Basia: dla mnie ten obszar jest nieograniczony taki graniastosłup nieskończony o podstawie a0a i dlatego mi się cały czas nie zgadza

Basia: ale się nie upieram może jest inaczej

Vizer: Zgadzam się z Tobą Basiu, jak dla mnie powinno być coś w stylu x + y + z = a. Na górze się pospieszyłem z rozwiązaniem i fakt brakuje jednej powierzchni do zamknięcia obszaru.