Planimetria, kiełbasa Alois~: Jeden z kątów czworokąta wpisanego w okrag ma miare 60^o , boki zawarte w ramionach tego kąta są równe. Wykaż, że suma długości pozostałych dwóch boków jest równa długości przekątnej poprowadzonej z wierzchołka o mierze 60^o

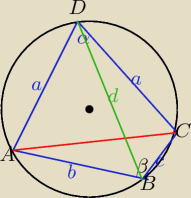
Basia: jakim trójkątem jest ACD ? jak jest wobec tego długość AC ? ile stopni ma kąt β ? odpowiedz najpierw na te pytania

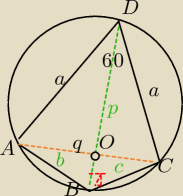
Mila: mamy wykazać, że b+c=p ∡ABC=120⁰ z własności czworokątów wpisanych w okrąg q=a, ΔACD jest równoboczny ∡DBC=∡DAC=60⁰ wpisane oparte na tym samym łuku. Z tw, cosinusów w ΔBCD a²=c²+p²−2pccos60=c²+p²−pc ∡ABD=120−60=60 a²=b²+p²−2bpcos60 a²=b²+p²−bp a²=c²+p²−pc porównując, mamy c²+p²−pc=b²+p²−bp c²−pc=b²−bp c²−b²−pc+bp=0 (c−b)(c+b)−p(c−b)=0 (c−b)(c+b−p)=0 c=b lub c+b=p Rozważ przypadek c=b

Basia: można szybciej jak już zauważyłaś, że ∡DBC = 60 to zauważ, że ∡DBA też = 60 czyli BD jest dwusieczną kąta CBA⇒1. b=c 2. BD musi być też dwusieczną kąta ADC czyli środek okręgu leży na BD ⇒ tr.DCB i DAB są prostokątne z kątami 30 i 60 p = 2b p = 2c 2p=2b+2c p = b+c

Basia: trochę źle to sformułowałam: ∡DBC = 60 i ∡DBA = 60 ⇒ BD jest dwusieczną ∡ABC ⇒ środek okręgu S∊BD ⇒ BD musi być też dwusieczną ∡ADC stąd mamy, że tr.BAD i tr.BCD są prostokątne z kątami ostrymi 30 i 60 ⇒ p = 2b i p=2c 2p = 2b+2c p = b+c

Alois~: Basia i Mila dzięki robie te zadania i robie nie nadążam z wykonaniem ich na czas i rozumieniem jednocześnie, coś słabo zaczynam widzieć ten mój wybór rozszerzonej matmy

Mila: Trening czyni mistrza.Powodzenia. To zadanie należy do trudnych, takie moje obserwacje po pracy z uczniami.

ICSP: albo tak : |AB| = |BC| = a oraz ∡ABC = 60^o co oznacza że z twierdzenia cosinusów :

	1
|AC|2 = a2 + a2 − 2*a*a*		= a2 + a2 − a2 = a2
	2

|AC| = a i teraz mam wykazać że : |BD| = |AD| + |CD| z twierdzenia Menelaosa mam że : |AC| * |BD| = |AB| * |CD| + |BC| * |AD| zatem podstawiając odpowiednio a * |BD| = a * |CD| + a* |AD| a * |BD| = a(|CD| + |AD|) |BD| = |AD| + |CD| c.n.u.

Alois~: Mila dziękuje ! ciężka praca być musi tak czy inaczej, ważne że takie dobre dusze tutaj czuwają nad nami w tych zmaganiach maturalnych

ICSP: z twierdzenia Ptolemeusza oczywiście

Basia: Alois~ nie poddawaj się. Oceniam Cię bardzo dobrze, przede wszystkim dlatego, że chcesz i umiesz myśleć. A to co najmniej połowa sukcesu. Chciałam Cię powolutku doprowadzić do samodzielnego rozwiązania tego zadania, ale Mila troszkę się pospieszyła. Chyba Milu jeszcze nie poznałaś dobrze Alois~. Trzeba jej dawać wskazówki i czekać cierpliwie. Odezwie się. Milu nie traktuj tego broń Boże jak jakiś zarzut. To tylko i tylko wyjaśnienie Pozdrawiam obie Panie

Basia: @ICSP Iliadę czytasz czy co ? Skąd Ci się wziął Menelaos ? Wiem, że poprawiłeś, ale ciekawa jestem skąd takie skojarzenie ?

ICSP: Zawsze mi się mylą te dwa twierdzenia ze sobą

Mila: ICSP, a trójkąt równoramienny z kątem 60 ⁰ miedzy ramionami zawsze jest równoboczny. Twierdzenie Ptolemeusza− dobrze że zastosowałeś, ale w LO mało kto o tym słyszy ( na początku III klasy, potem będą stosować). No tutaj pięknie wychodzi teza. (trochę inaczej oznaczyłeś niż Basia i ja− oznaczenia zupełnie przypadkowo zbieżne) WG moich oznaczeń p*q=p*a p*a=c*a+b*a p=c+b

Mila: DLa ALi. http://pl.wikipedia.org/wiki/Twierdzenie_Ptolemeusza