pomocy Krzysiek: W zaleznosci od parametru m wyznacz liczbe punktow wspolnych okregu (x−1)²+(y+3)²=3 i prostej x+y−m=0. jak to zrobic Czy mam z drugiego rownania np wyliczyc x i wstawic do pierwszego czy jak

Krzysiek: jesli m=0 to prosta bedzie przechodzic przez poczatek ukladu wspolrzednych, uzyc tego jakos

Krzysiek: dokladne rozw poprosze

Krzysiek: moze Eta mi pomoze

Krzysiek: pomocy

pazio: dobra ja się zlituję

Krzysiek: ojej dzieki pazio

Krzysiek: no bo nie wiem czy tak czy tak, a nie chce mi sie matoda prob i bledow

Krzysiek: rob rob to potem sobie obczaje

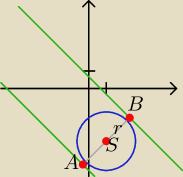
Bogdan: Prosta: x + y − m = 0. Okrąg: (x − 1)² + (y + 3)² = 3. Prosta ma jeden punkt wspólny z okręgiem wtedy, gdy jest styczną okręgu. Odległość od punktu styczności do środka okręgu jest równa długości promienia okręgu. Środek okręgu S = 1, −3), długość promienia r = √3. |AS| = |BS| = r. Stosujemy wzór na odległość punktu od prostej.

|1*1 − 3*1 − m|
	= √3 ⇒ |−m − 2| = √6 ⇒ |m + 2| = √6
√1 + 1

Rozwiąż równanie: |m + 2| = √6, otrzymasz dwie wartości parametru m.

pazio: (x−1)² + (y+3)² = 3 i[coś mi się e znaczkami pojebało] y = −x +m x² − 2x + 1 + x² − 2x(m+3) + (m+3)² = 3 2x² − 2(1+m)x + m² + 6m + 7 = 0 Δ = 4(m+1)² − 4(m²+ 6m + 7) no i w zależności od delty masz takie a nie inne rozwiązania

pazio: Bogdan, nie do końca, nie uwzględniasz siecznych w swoim rozwiązaniu

Damian: uwzględnia bo zrobi przedział

pazio: aaaa sprytnie

Damian: Bogdan wie co robi

pazio: też prawda

Bogdan: Podałem tylko jedną z sytuacji w tym zadaniu licząc na to, że Krzysiek z pozostałymi sytuacjami sobie poradzi. Nie podałem rozwiązania dla dwóch punktów wspólnych i dla braku punktów. Trzeba w tych dwóch przypadkach rozwiązać nierówności: |m + 2| = √}, |m + 2| > √6.

Bogdan: Chochlik: |m + 2| < √6 i |m + 2| > √6

Bogdan: Krzyśku, podaj Twój końcowy wynik

Damian: bogdanie moge ja

Bogdan: Proszę bardzo Damianie, skoro Krzysiek milczy.

Damian: m+2 <√6 i m+2> −√6 m< √6 −2 i m > −√6−2

xax:

daveustro: Mi wyszedł taki wynik: 2 pkty. wspólne dla m∊(−2−√6, −2+√6) 1 pkt. wspólny dla m=−2−√6 v m=−2+√6 0 pktów. wspólnych dla m∊(−∞, −2−√6) v m∊(−2+√6, +∞) Ma ktoś też taki wynik

Krzysiek: mi wyszlo tak: sa 2 punkty wspolne gdy m∊(−√6−2;√6−2) jest 1 punkt wspolny gdy m=−√6−2 lub m=√6−2 i brak wspolnych punktow dla m∊(−∞;−√6−2)∪(√6−2;+∞) czyli tak jak deveustro to chyba dobrze

Krzysiek: Bogdanie, milczalem bo mnie nie bylo