? Patryk: dla jakich wwartosci parametru p równe pierwiastki równania naleza do przedziału <−√5;√5> ? zapomniałem warunku

Patryk: x²−2√2x+p²+1=0

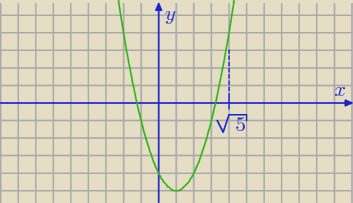
Godzio: f(√5) > 0 f(−√5) > 0 Δ > 0 (domyślam się, że w poleceniu były "różne" a nie "równe" )

Patryk: f(√5)>0 dlaczego tak ?

Patryk:

	√2		√2
w odpowiedziach mam (−1;−		;>U<		;1) ale nie wychodzi
	2		2

Godzio: Warunki odczytujemy z wykresu, Zapomniałem dodać, jeszcze jeden warunek: −√5 < x_w < √5, żeby nam nie wyleciał za przedział

Patryk: ale ten jest automatyczne spełniony bo xw=√2 dla kazdego

Patryk: dlaczego moje odpowiedzi się nie zgadzają ?

Godzio:

⎧	f(√5) ≥ 0
⎜	f(−√5) ≥ 0
⎨	−√5 < xw < √5 (zawsze spełniony)
⎩	Δ > 0

Δ = 8 − 4p² − 4 = − 4p² + 4 > 0 ⇒ p² < 1 ⇒ p ∊ (−1,1) Na pewno dobrze polecenie jest ? Bo z tym √5 to nie specjalnie coś takiego wychodzi ...

Patryk: Polecenie prawdziwe; liczby x₁ i x₂ są róZnymi pierwiastkami równania x²−2√2+p²+1=0.Dla jakich wartosci parametru p punkt (x₁, x₂) należy do koła o środku S=(0,0) i promieni √5 chyba juz widze co zrobiłem zle

Godzio: Ehhh Pierwiastki muszą spełniać równanie okręgu x₁² + x₂² ≤ 5 ⇒ (x₁ + x₂)² − 2x₁x₂ − 5 ≤ 0 8 − 2p² − 2 − 5 ≤ 0 2p² ≥ 1

	√2		√2
p2 ≥ 1 ⇒ p ∊ (−∞, −		>U<		,∞) + warunek z delty i masz odpowiedź
	2		2

Godzio:

	1
p2 ≥		oczywiście
	2

Patryk: dzięki,takie proste ,a takie trudne

Patryk: Wykaż,że jeśli liczby a i b są różne,to równanie x²+y²+ax+by+0,5ab=0.jest równaniem okregu.podaj jego promień . robie tak

	a		b		1		1		1
(x+		)2+(y+		)2=		a2+		b2−		ab
	2		2		4		4		2

1		1		1
	a2+		b2−		ab>0 czy warunek jest dobry ?
4		4		2

Godzio: Tak, pokaż, że to jest stale dodatnie

Patryk: razy 4 a²+b²−2ab>0 (a−b)²>0

Patryk: no tyle umiem

Godzio: No + komentarz i zaliczone

Patryk: ooo,