Podstawą ostrosłupa ABCD jest trójkąt równoboczny a: Podstawą ostrosłupa ABCD jest trójkąt równoboczny o boku długości √2. Wszystkie ściany booczne są równoramiennymi trójkątami prostokątnymi. Punkt P został wybrany wewnątrz ostrosłupa w ten sposób, że wysokości ostrosłupów ABDP, BCDP, ACDP, ABCP opuszczone z wierzchołka P mają tę samą długość H. Sporządź rysunek i oblicz H. Nie wiem jak zrobić to zadanie. Będę wdzięczny za pomoc. Pozdrawiam

pazio: postaram się coś wykombinować

luck00: ok poczekam

luck00: no i co, coś wymyśliłeś?

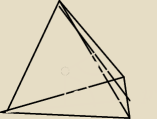
pazio: ten rysunek jest dziwny. nie potrafię nic z nim zrobić. H − to te małe wysokości h − wysokość ostrosłupa porównujesz objętości:

1		(√2)2√3		1		(√2)2√3
	*		*H =		h(		+ 3Pśb)
3		4		3		4

ściany boczne to równoramienne trójkąty prostokątne. w nich przeciwprostokątną jest √3

	√6
czyli bok ma długość
	2

	1		√6		√6
Pśc =		*		=
	2		2		4

wracasz do objętości:

√3		1		(√3		√6
	*H =		h(		+ 3*		)
6		3		2		4

√3		h		2√3+3√6
	*H =		*
6		3		4

	6h(2√3+3√6)
H =
	12√3

teraz szukasz h. możesz go obliczyć z trójkąta: krawędź ostrosłupa, wysokość ostrosłupa,

	1
		wysokości podstawy:
	3

	√6		√6
h2 = (		)2 + (		)2
	2		6

	6		6
h2 =		+
	4		36

	60
h2 =
	36

	√15
h =
	3

podstawiasz do wzoru i masz

pazio: owszem, wymyśliłAM

luck00: Dłuższy czas myślałem nad tym zadaniem. Dzięki wielkie. Sory za EŚ, ale trudno dojść po loginie z jaka płcią mam przyjemność rozmawiać Pozdrawiam

imię lub nick: "ściany boczne to równoramienne trójkąty prostokątne. w nich przeciwprostokątną jest √3 " √2, pazio

pazio: luz, przywykłam już ludzie nawet mówią, że pazio brzmi męsko

imię lub nick: krawędź będzie równa 1

luck00: pazio, a Ty jak tak trzaskasz te wszystkie zadania to na co się wybierasz?

luck00: Tak, imię lub nick masz chyba rację