równania nierówności d4mian: 1.dopasuj współczynnik a by nierówność się zgadzała log_(4a−1) 7 > log_(4a−1) 12 2. rozwiąż graficznie |x−3| > 1

Mila: 1) 0<4a−1<1 [podstawa=(4a−1) jest z przedziału (0,1)] rozwiąż 2) odległość liczb od 3 jest większa niż jedna jednostka

Vizer: zad. 1 Gdyby (4a − 1) > 1 to funkcja logarytmiczna byłaby rosnąca i nierówność prezentowałaby się tak : 7 > 12 co nie jest prawdą. Właściwym wnioskiem jaki trzeba tu wysnuć, to funkcja logarytmiczna musi być malejąca, więc podstawa logarytmu musi spełniać nierówności : 0 < 4a − 1 < 1 Rozwiązujemy dalej : 0 < 4a − 1 ∧ 4a − 1 < 1

	1		1
a >		∧ a <
	4		2

	1		1
a∊(		,		)
	4		2

I dla takich a, nasza nierówność wejściowa rozwiązuje się tak : 7 < 12 co jest prawdą.

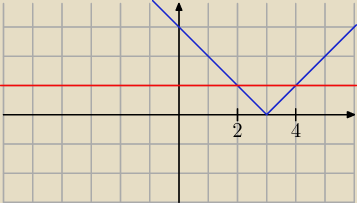
Vizer: Albo narysować sobie wykresy i zobaczyć na jakich przedziałach funkcja y = |x − 3| (na niebiesko) jest wyżej od funkcji y = 1 (na czerwono) oczywiście z wyłączeniem punktów, gdzie te dwie funkcje się przecinają, bo mamy nierówność ostrą.