Jak rozwiązać to równanie? Maron: √x + y = 7 √y + x =11

ICSP: y = 4 x = 9

Maron: Niestety z tego co wiem to nie są dobre odpowiedzi Też mi tak wyszło .... Nie znam odpowiedzi ale wiem ze to jest złe. Spotęgowanie 1 linijki daje : x + y² = 49 a wiec jesli przyjąć te odpowiedzi podane wyżej wychodzi, że: 9 + 4² = 49 równanie jest sprzeczne. Może ktoś wymyśli jak to rozwiązać...

Buuu: Spotęgowanie 1. linijki daje: (√x + y)² = 49 x + 2y√x + y² = 49 9 + 2*4*3 + 16 = 49 9 + 24 + 16 = 49 49 = 49

ICSP: √9 + 4 = 3 + 4 = 7 √4 + 9 = 3 + 9 = 11 nadal sądzisz że są to złe odpowiedzi ?

asdf: Tak, to jest złe bo zapomniałeś o dziedzinie, całe zadanie do dupy....

ICSP: −₋ podałem tylko odpowiedzi a nie rozwiązanie zadania

konrad: przecież 4 i 9 należą do dziedziny, wszytko jest ok

Maron: Gdyby to było takie proste to bym tego zadanie nie wrzucał tutaj ... Jeśli znajomy który zdawał rozszerzenie z matmy nie potrafi tego ogarnąć to chyba nie jest to takie proste ... odpowiedzi Twoje pasują ale nie sa dobre bo odpowiedz musi zawsze pasować nieważne co z równaniem byśmy zrobili jak pisałem wyżej. Wiem że się czepiam ale 3+9 nie daje 11.

asdf: To może idź jeszcze do twojego kumpla, żeby nauczył Ciebie podstawiania

ICSP: √4 = 3 ?!

konrad: ICSP się po prostu pomylił i napisał 3 zamiast 2, co nietrudno się domyśleć że powinno być 2 skoro jest √4

Buuu: Wiem, że się czepiam, ale źle spotęgowałeś 1. linijkę Maron http://www.wolframalpha.com/input/?i=x^%281%2F2%29+%2B+y+%3D+7++%26+y^%281%2F2%29+%2B+x+%3D+11

Maron: Zwracam honor wszystkim którzy tutaj się wypowiedzieli ... Wprowadzenie w błąd przez pewna osobę + gorszy dzień .... Jeśli ktoś ma taką możliwość proszę o dokładniejsze wytlumaczenie skad sie to wzieło ... Sorki za akcje ....

asdf:

Maron: W sensie skąd się rozwiazanie wzieło a nie moje wypowiedzi

asdf: √x + y = 7 √y + x = 11 y = 7 − x^1/2 √7 − x^1/2 + x = 11 7^1/2 − x^1/4 + x = 11 x − x^1/4 = 11 − 7^1/2 t = x^1/4 t⁴ − t − 11 + 7^1/2 = 0 jak tu znaleźć pierwiastek?

b.: asdf 22:53: √7−x^1/2 ≠ √7 − ⁴√x

ZKS: Ja bym raczej tak zaczął. x , y ≥ 0 {√x = 7 − y ⇒ x = (7 − y)² zał. 0 ≤ y ≤ 7 {√y + x = 11 √y + (7 − y)² = 11 y² − 14y + √y + 38 = 0 √y = t ≥ 0 t⁴ − 14t² + t + 38 = 0

asdf: @b. racja √7 − x^1/2 + x = 11 podpowiedź można?

asdf: ZKS, ale co z tym fantem ?

ZKS: Jeszcze założenie co do t. √y = t (0 ≤ t ≤ √7)

ZKS: Poszukaj pierwiastków w dzielnikach wyrazu wolnego podpowiedź szukaj tylko dla 1 i 2 patrz założenia do t.

ZKS: I co jest pierwiastkiem?

asdf: To nie mój poziom

b.: 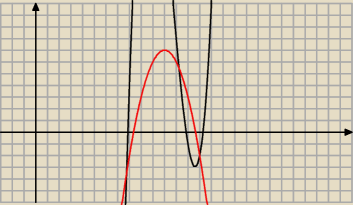√7−x^1/2 = 11−x musi być x≤11, dalej 7−√x = 121 − 22x + x² −114+22x−x² = √x lewa strona musi być nieujemna, czyli x pomiędzy 11−√7 a 11+√7 (czerwony wykres), i dalej (−114+22x−x²)² = x x⁴−44x³+712x²−5017x+12996 = 0 (wg wolframa) (x−9)(x³−35x²+397x−1444) = 0 (wg wolframa) drugi czynnik narysowany na czarno jak widać, w ten sposób to się tego raczej ręcznie nie rozwiąże, więc trzeba raczej odgadnąć rozwiązanie (co zostało już zrobione), a potem pokazać, że innych rozwiązań nie ma

ZKS: To sprawdzasz dla t = 1 1⁴ − 14 * 1² + 1 + 38 = 1 − 14 + 1 + 38 ≠ 0 więc 1 nie jest pierwiastkiem równania t⁴ − 14t² + t + 38 = 0 zostało nam t = 2 2⁴ − 14 * 2² + 2 + 38 = 16 − 56 + 40 = 0 czyli pierwiastkiem równania t⁴ − 14t² + t + 38 = 0 jest t = 2 √y = 2 ⇒ y = 4 x = (7 − 4)² ⇒ x = 3² ⇒ x = 9 ostatecznie x = 9 ∧ y = 4.

b.: sposób ZKS jest o niebo lepszy, ale jeszcze trzeba podzielić podany wielomian stopnia 4 przez (t−2) i sprawdzić, że powstały wielomian stopnia 3 nie ma pierwiastków dla tych t, dla których wyjściowy układ ma sens

ICSP: da się to rozwiązać ręcznie. Trzeba tylko znać dobrze definicję pierwiastka arytmetycznego.

b.: zgadza się, da się, tylko nie w ten sposób w jaki ja pisałem np. mamy √7−x^1/2 + x =11 podstawmy u=√x √7−u+u² = 11 (u ∊ [0,7]) policzmy pochodną:

	−1		4u √7−u − 1
		+ 2u =		> 0 dla u ∊ [1,6]
	2√7−u		2√7−u

więc na przedziale [1,6] rozwiązanie jest maksymalnie jedno (odgadujemy je: u=3, co daje x=9, y=4). A na przedziałach [0,1) oraz (6,7] od razu widać, że rozwiązań nie ma (lewa strona jest za mała lub za duża).

ZKS: t⁴ − 14t² + t + 38 = (t − 2)(t³ + 2t² − 10t − 19) oraz t ∊ [0 ; √7] (√7 ≈ 2.65) Z twierdzenia Darboux pokazujemy że równanie t³ + 2t² − 10t − 19 = 0 ma pierwiastki nie należące do dziedziny. f(−3) * f(−4) < 0 więc kolejny pierwiastek jest w przedziale (−4 ; −3) f(−2) * f(−1) < 0 następny znajduje się w przedziale (−2 ; −1) f(3) * f(4) < 0 ostatni pierwiastek należy do przedziału (3 ; 4) Czyli jeden pierwiastek spełnia równanie i należy do naszej dziedziny.

Vax: Dodając stronami dostajemy x+√x = 18−(y+√y), ale f(x) = x+√x jest funkcją ściśle rosnącą dla x>0, więc po lewej stronie mamy funkcję ściśle rosnącą, a po lewej ściśle malejącą, więc mogą się przeciąć jedynie w 1 punkcie, pozostaje zgadnąć, że (x,y) = (9,4)

b.: ładne rozwiązanie nawiasem mówiąc, jak to zadanie zobaczyłem gdy nie było jeszcze żadnych odpowiedzi, to sobie pomyślałem, że lepiej nie będę go rozwiązywał, bo na pewno ktoś inny zrobi to lepiej − a później coś mnie podkusiło... ech...