Oblicz pole boczne i objętość graniastosłupa Kasia: W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 39 cm, a krawędź boczna tworzy z płaszczyzną podstawy kąt 60 stopni. Oblicz pole powierzchni bocznej i objętość graniastosłupa.

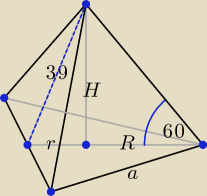
Bogdan: a − długość boku trójkąta równobocznego będącego podstawą ostrosłupa, a > 0 r − długość promienia okręgu wpisanego w trójkąt równoboczny o boku a, R − długość promienia okręgu opisanego na trójkącie równobocznym o boku a.

	1		1
r =		a√3, R =		a√3
	6		3

H		1
	= tg60o ⇒ H =		a√3*√3 = a, tg60o = √3
R		3

Z twierdzenia Pitagorasa:

	3		39
H2 + r2 = 39 ⇒ a2 +		a2 = 39 ⇒		a2 = 39 ⇒ a2 = 36 ⇒ a = 6
	36		36

a = 6 ⇒ H = 6 Objętość i pole powierzchni ostrosłupa (nie graniastosłupa) policzysz bez truności.