Styczna równolegla do wykresu Pomocy ! mateusz: Nikt nie moze mi pomoc...jak zrobic zadanie :Styczna równoległa do wykresu : f(x)=x² y= −2x

Gustlik: Musisz podać co najmniej jedną współrzędną punktu styczności, np. napisz równanie stycznej do wykresu f(x)=x² w punkcie x₀=... np. 2. Bez tego się nie da rozwiązać.

pigor: ... otóż szukasz stycznej do paraboli y=x² w postaci y= −2x+b , czyli takiej, że równanie x²= −2x+b ma dokładnie 1 rozwiązanie ⇔ x²+2x−b=0 i Δ=4+4b=0 ⇒ 4b=−4 ⇔ ⇔ b=−1 , zatem y= −2x−1 ⇔ 2x+y+1=0 − szukane równanie stycznej ...

Gustlik: Aha, już wiem o co chodzi − ma być styczna do wykresu f(x)=x² równoległa do wykresu y=−2x. Pisz bardziej precyzyjnie, bo później trzeba się domyślać, o co kaman. Licze pochodną funkcji f(x) f'(x)=(x²)'=2x Współrzynnik kierunkowy stycznej jest rowny wartości pochodnej danej funkcji liczonej w punkcie styczności. Czyli a=f'(x)=−2, bo styczna ma byc równoległa do prostej y=−2x, czyli musi mieć taki sam wspołczynnik kierunkowy. 2x=−2 /:2 x=−1 ← to współrzędna "x" punktu styczności. Szukam współrzędnej y y=f(−1)=(−1)²=1, czyli P=(−1, 1) ← punkt styczności. Styczna ma równanie y=−2x+b 1=−2*(−1)+b 1=2+b b=−1 Odp: y=−2x−1

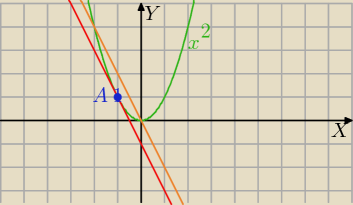
Mila: styczna y=−2x+b x²=−2x+b x²+2x−b=0 równanie ma dokładnie jedno rozwiązanie Δ=4+4b=0 b=−1 s: y=−2x−1 (czerwony wykres) [Punkt styczności : x²+2x+1=0 x=−1 y=x²; y=1 A=(−1,1)

mateusz: aaaaa dziekujeeee Jesteście wielcy