Pola figur podobnych Paula: W kwadracie, którego bok ma długość a, poprowadzono proste równoległe do jednej z przekątnych w równych od niej odległościach. Podzieliły one ten kwadrat na trzy części o równych polach. Oblicz odległość tych prostych od przekątnej kwadratu. Proszę o pomoc.

Buuu:

	P'
k2 =
	P

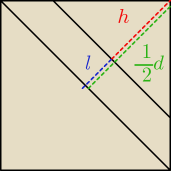
k² = 0,5 k = ^√2₂

h
	= k
0,5d

h = k * ¹₂d

	√2d
h =
	4

h = U{p[2}a√2}{4} h = ¹₂a l = ¹₂d − h = ¹₂a√2 − ¹₂a = ¹₂a(√2 − 1)

Buuu: 3 linijka od dołu powinna być:

	√2a√2
h =
	4

Nienor:

	1		3
Pola CGFA i CHEA są sobie równe. Pole GFAC=		Pola GFB. Pole CAB=		pola CAB.
	2		2

	1
Jeżeli d jest odległością od przekątnej to h trójkąta GFB wynosi		a√2−d
	2

1		3		1		1
	a2=		*		b*(		a√2−d)
2		2		2		2

I

1		1		1		1
	*		(a√2+b)d=		b*(		a√2−d)
2		2		2		2