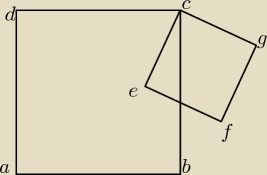
Dane są kwadraty dk1993: Dane są kwadraty ABCD i CEFG wykaż, że DE=BG

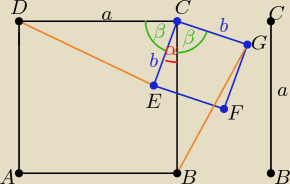Eta: W trójkątach DEC i BGC : β=90^o−α= |∡BCG|= |∡DCE| −−− jest kątem zawartym między bokami DC i EC oraz BC i GC i |DC|=|BC|=a i |EC|= |CG|=b zatem trójkąty DEC i BGC są przystające z cechy ( b,k,b) to: |DE|= |BG| c.n.u