dziedzina wielomiany adzior: czesc, nie umiem zrobic zadania z wielomianow o tresci Wyznacz dziedzinę z wyrażenia:

	√16−x2
W(x) =
	x3+x−10

Wiem, że tylko mianownik trzeba zrobić x³+x−10 ale nie mam pojęcia jak

Artur_z_miasta_Neptuna: przyrównujesz mianownik do zera i obliczasz dla jakiego 'x' to równanie jest spełnione

sushi_gg6397228: a jak szukaliscie na lekcji miejsc zerowych dla wielomianu?

asdf: mianownik musi być różny od zera Jeżeli w liczniku jest pierwiastek to musi on być ≥ 0 16 − x² ≥ 0 oraz: x³ + x − 10 ≠ 0 Patrzysz na część wspólną i masz dziedzine

adzior: Chodzi mi o to, jak obliczyć te x³ + x − 10 ≠ 0 bo w x²≥16 wyszlo x ≥ 4 lub x ≤ −4, tak ?

ICSP: x³ +x − 10 = 0 x³ − 2x² + 2x² − 4x + 5x − 10 = 0

adzior: Przeciez to jest to samo... ?

ICSP: ale teraz możesz to ładnie pogrupować

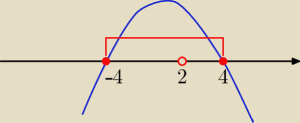
Eta: x³+x−10=0 W(2)= 8+2−10=0 czyli x= 2 jest pierwiastkiem tego równania podziel (x³+x−10) : (x−2) =.... otrzymasz rozkład mianownika (x−2)(x²+2x+5) ,Δ<0 −−−brak pozostałych pierwiastków w zb. R D: 16−x²≥0 i x−2≠0 ( 4−x)(4+x)≥0 ⇒ x€ <−4, 4> i x≠2 to: D= <−4,4> \ {2} Teraz przepisuj .........gotowca

adzior: Dzięki, tak mi jest poprostu łatwiej zrozumieć − na konkretnych przykładach, i już rozumiem