Rozwiąż równania i nerówności z wartością bezwzględną
Crowely: −3 < |5 − x| < 2
|x + 3| > |x −2|
|5x − 2| −3|4 − 2x| <2,5
Proszę o pomoc bo naprawdę mam z tym problem a we wtorek mam kartkówkę z tego na rozszerzeniu
23 wrz 15:47
Crowely: z góry dzięki

!
23 wrz 15:48
krystek: a) I5−xI<2⇔5−x<2 i 5−x>−2 ponieważ I5−xI>−3 dla każdego x
23 wrz 15:50
krystek: b) musisz rozpatrzyć w przedziałach (−∞,−3) U<−3,2) U <2,∞) analog. c)
23 wrz 15:51
Crowely: a więc w przykładzie A
w 1 równaniu bedzie 8>x>3 i część wspolna to <5 ,8)
w 2 równaniu będzie 2< x < 7 i część wspólna to (2 ,5)
23 wrz 16:20
pigor: ... a więc np. tak :
−3<|5−x|<2 ⇔ −3< |x−5|< 2 ⇔ |x−5| > −3 ∧ |x−5|< 2 ⇔ x∊R ∧ −2< x−5< 2 ⇔
⇔ −2+5< x< 2+5 ⇔
3< x< 7 ⇔
x∊(3;7) ;
−−−−−−−−−−−−−−−−−−−−−−
|x+3| >|x−2| ⇔ |x−2|< |x+3| ⇔ −(x+3)<x−2<x+3 ⇔ −x−3+2<x< x+5 ⇔ x<x+5 ∧ x>−x−1 ⇔
⇔ 0<5 ∧ 2x>−1 ⇔ x∊R ∧ x>−
12 ⇔
x>−12 ⇔
x∊(−12;+∞) ;
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
|5x−2|−3|4−2x|< 2,5 pobaw się sam w odpowiednich przedziałach . ...

23 wrz 16:47
Crowely: Dlaczego w tym pierwszym przykładnie jest −2 < x −5 < 2 a nie naprzykład −3 < x−5< 3?
23 wrz 17:10
PW: Z a w s z e trzeba rzucić okiem na sens zadania, zanim zacznie się stosować schematy.
W pierwszym mamy do czynienia z "podpuchą" autora zadania. Zastanów się: co to za informacja
−3 < |5−x|?
Ano żadna, bo z definicji wartość bezwzględna jest nieujemna − nie ma co się nad tym
zastanawiać, ta nierówność jest prawdziwa dla każdej x. Pozostaje rozwiązać
.|5−x| < 2,
czyli
−2 < 5−x < 2;
dodajemy stronami −5:
−7 < −x < −3,
mnożymy stronami przez −1:
7 > x > 3.
Odpowiedź: x ∊ (3, 7).
23 wrz 22:23
Gustlik:
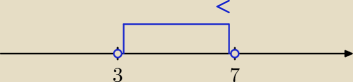
−3 < |5 − x| < 2
Masz "przestawione" odejmowanie, skorzystaj z |a−b|=|b−a|, wygodniej się robi, gdy "x" jest
pierwszy, a nie na koncu.
−3 < |x − 5| < 2
Rozbijasz na koniunkcję 2 nierówności:
(1) |x−5|>−3 ⇒ x∊R, bo moduł zawsze jest nieujemny, a więc większy od liczby ujemnej,
(2) |x−5|<2
Rozwiązujesz jak równanie − liczba spod modułu zmienia znak, a tę z prawej strony raz dodajesz,
a potem odejmujesz.
x=5±2
x=7 v x=3
Przedział rysujesz od prawego końca i idziesz zgodnie ze znakiem nierówności < czyli w lewo, a
na lewym końcu się zamknie.
x∊(3, 7)
Rozwiązaniem jest częśc wspólna (1) i (2), a więc x∊(3, 7), bo w (1) było x∊R.
23 wrz 22:31
Gustlik:
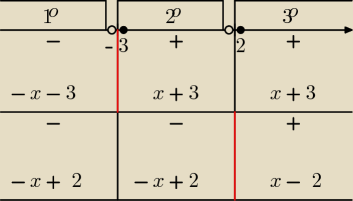
|x + 3| > |x −2|
Jak są dwa (i więcej) modułów, to wyznaczam miejsca zerowe każdego modułu i otrzymuję:
x=−3 i x=2
Potem metoda "osi i tabelki" − korzystasz z faktu, że każde wyrażenie typu x−a jest ujemne na
lewo od swojego miejsca zerowego
(zaznaczyłem czerwoną linią), a dodanie na prawo od
niego. A więc na lewo od miejsca zerowego moduł danego wyrażenia opuszczamy ze zmianą znaku, a
na prawo − bez zmiany znaku.
Z osi i tabelki łatwiej sie odczytuje − metoda przyjazna dla wzroku, uczeń po prostu widzi, co
robi − łatwiej jest ułożyć przypadki.
Teraz jedziesz "kolumnami", a założeniami są przedziały zaznaczone nad daną kolumną:
1
o) −x−3>−x+2 i x∊(−
∞, −3)
2
o) x+3>−x+2 i x∊<−3, 2)
3
o) x+3>x−2 i x∊<2, +
∞)
Teraz rozwiązujesz te 3 przypadki − rozwiązaniem każdego przypadku jest część wspólna
rozwiązania nierówności i założenia.
ad 1
o)
−x−3>−x+2 i x∊(−
∞, −3)
−x+x>2+3
0>5 ⇒ sprzeczność ⇔ x∊∅
ad 2
o)
x+3>−x+2 i x∊<−3, 2)
x+x>2−3
2x>−1 /:2
| | 1 | | 1 | |
x>− |
| i i x∊<−3, 2) ⇒ x∊(− |
| , 2) |
| | 2 | | 2 | |
ad 3
o)
x+3>x−2 i x∊<2, +
∞)
x−x>−2−3
0>−5 ⇒ tożsamość ⇒ x∊R i x∊<2, +
∞) ⇔ x∊<2, +
∞) (przy tożsamości całe założenie jest
rozwiązaniem)
Na końcu rozwiązania przypadków sumujemy:
| | 1 | | 1 | |
1o U 2o) U 3o) ⇔ x∊∅U(− |
| , 2)U<2, +∞) ⇔ x∊(− |
| , +∞) |
| | 2 | | 2 | |
23 wrz 22:52
Gustlik: |5x − 2| −3|4 − 2x| <2,5
W drugim module masz znowu "przestawione" odejmowanie − skorzystaj z |a−b|=|b−a|, jak w
przykładzie pierwszym, bo łatwiej jest z "x"−em na początku, otrzymasz:
|5x − 2| −3|2x − 4| <2,5 /*2 (aby pozbyć się ułamka z prawej strony)
2|5x−2|−6|2x−4|<5
Teraz wyznacz miejsca zerowe modułów i "osią i tabelką", jak przykład drugi.
23 wrz 22:56
PW: Napiszę , jak rozwiązać b) tak, żeby nie stosować schematu "podziału na przedziały".
|x+3| > |x−2|.
Sprawdzamy, że liczba 2 spełnia nierówność:
|2+3| > |2−2| − zdanie prawdziwe.
Dla pozostałych x prawa strona nierówności jest liczbą dodatnią, możemy więc podzielić obie
strony nierówności przez |x−2| nie zmieniając nierówności na przeciwną:
| | |x+3| | | x+3 | | x−2+5 | | 5 | |
|
| > 1 ⇔ | |
| | > 1 ⇔ | |
| | > 1 ⇔ |1 + |
| | >1 ⇔ |
| | |x−2| | | x−2 | | x−2 | | x−2 | |
| | 5 | | 5 | | 5 | | 5 | |
1 + |
| >1 ∨ 1 + |
| < −1 ⇔ |
| > 0 ∨ |
| < −2. |
| | x−2 | | x−2 | | x−2 | | x−2 | |
W pierwszej nierówności ułamek o liczniku 5 ma być dodatni, więc mianownik też musi być
dodatni.
Druga nierówność jest spełniona, gdy mianownik jest ujemny (przy mnożeniu pamiętamy o zmianie
nierówności na przeciwną).
x > 2 ∨ x−2 < 0 ∧ 5 > −2
. (x−2)
x >2 ∨ (x < 2 ∧ 5 > −2x +4)
x > 2 ∨ (x < 2 ∧ 1 > −2x)
| | 1 | |
x > 2 ∨ (x < 2 ∧ x > − |
| ) |
| | 2 | |
| | 1 | |
x ∊ (2,∞) ∨ x ∊ (− |
| ,2). |
| | 2 | |
Pamiętając o tym, że liczba 2 też spełnia nierówność, możemy udzielić odpowiedzi:
| | 1 | | 1 | |
Rozwiązaniem nierówności jest (− |
| ,2> ∪ (2,∞) = (− |
| , ∞). |
| | 2 | | 2 | |
Okazuje się, że można rozwiązać nie rozpatrując "przypadków", czego też nie lubię.
23 wrz 23:54
pigor: ... no to jeszcze np. tak :
|x+3| >|x−2| ⇔ |x+3|
2 >|x−2|
2 ⇔ (x+3)
2−(x−2)
2 >0 ⇔
⇔ (x+3−x+2)(x+3+x−2) >0 ⇔ 2x+1 >0 ⇔
x > −12 ⇔
x∊(−12;+∞). ...

24 wrz 00:03
Eta:

dla
pigora 
24 wrz 00:10
Gustlik:
 PW
PW, ja też nie lubie podziału na przedziały, ale tego robionego "szkolną" metodą. Dlatego
opracowałem metodę "osi i tabelki" bo z tego te przedziały i przypadki się bardzo szybko
odczytuje, a tabelka nie jest skomplikowana.
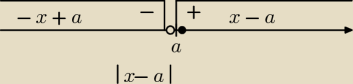
Korzystam z "graficznej" interpretacji definicji wartości bezwzględnej, zamiast sie rozpisywać,
że
|x−a|={x−a, gdy x−a≥0⇔x≥a
{−x+a, gdy x−a<0⇔x<a
to rozrysowałem to sobie w sposób przedstawiony na rysunku i na lewo od miejsca zerowego takie
wyrażenie (x−a) jest ujemne, więc tam opuszczam moduł ze zmianą znaku, a na prawo od miejsca
zerowego wyrażenie (x−a) jest dodatnie, więc opuszczam moduł bez zmiany znaku, a założenia
odczytuje z przedziałów.
Stąd metoda "osi i tabelki", którą polecam, bo jest pzrejrzysta.
Pozdrawiam

24 wrz 00:10
Gustlik: Pigor, bardzo dobra metoda, ale dla przypadków, gdy gdy poza dwoma modułami nic nie ma w
równaniu czy nierówności, ciężko by się tą metodą robiło przykład trzeci, bo tam jest z prawej
strony 2,5. Metoda "osi i tabelki" jest bardziej uniwersalna, poza tym można nią rozwiązywać,
gdy w modułach są funkcje kwadratowe lub wielomiany jeszcze wyższych stopni.
24 wrz 00:13
 !
!

 −3 < |5 − x| < 2
Masz "przestawione" odejmowanie, skorzystaj z |a−b|=|b−a|, wygodniej się robi, gdy "x" jest
pierwszy, a nie na koncu.
−3 < |x − 5| < 2
Rozbijasz na koniunkcję 2 nierówności:
(1) |x−5|>−3 ⇒ x∊R, bo moduł zawsze jest nieujemny, a więc większy od liczby ujemnej,
(2) |x−5|<2
Rozwiązujesz jak równanie − liczba spod modułu zmienia znak, a tę z prawej strony raz dodajesz,
a potem odejmujesz.
x=5±2
x=7 v x=3
Przedział rysujesz od prawego końca i idziesz zgodnie ze znakiem nierówności < czyli w lewo, a
na lewym końcu się zamknie.
x∊(3, 7)
Rozwiązaniem jest częśc wspólna (1) i (2), a więc x∊(3, 7), bo w (1) było x∊R.
−3 < |5 − x| < 2
Masz "przestawione" odejmowanie, skorzystaj z |a−b|=|b−a|, wygodniej się robi, gdy "x" jest
pierwszy, a nie na koncu.
−3 < |x − 5| < 2
Rozbijasz na koniunkcję 2 nierówności:
(1) |x−5|>−3 ⇒ x∊R, bo moduł zawsze jest nieujemny, a więc większy od liczby ujemnej,
(2) |x−5|<2
Rozwiązujesz jak równanie − liczba spod modułu zmienia znak, a tę z prawej strony raz dodajesz,
a potem odejmujesz.
x=5±2
x=7 v x=3
Przedział rysujesz od prawego końca i idziesz zgodnie ze znakiem nierówności < czyli w lewo, a
na lewym końcu się zamknie.
x∊(3, 7)
Rozwiązaniem jest częśc wspólna (1) i (2), a więc x∊(3, 7), bo w (1) było x∊R.
 |x + 3| > |x −2|
Jak są dwa (i więcej) modułów, to wyznaczam miejsca zerowe każdego modułu i otrzymuję:
x=−3 i x=2
Potem metoda "osi i tabelki" − korzystasz z faktu, że każde wyrażenie typu x−a jest ujemne na
lewo od swojego miejsca zerowego (zaznaczyłem czerwoną linią), a dodanie na prawo od
niego. A więc na lewo od miejsca zerowego moduł danego wyrażenia opuszczamy ze zmianą znaku, a
na prawo − bez zmiany znaku.
Z osi i tabelki łatwiej sie odczytuje − metoda przyjazna dla wzroku, uczeń po prostu widzi, co
robi − łatwiej jest ułożyć przypadki.
Teraz jedziesz "kolumnami", a założeniami są przedziały zaznaczone nad daną kolumną:
1o) −x−3>−x+2 i x∊(−∞, −3)
2o) x+3>−x+2 i x∊<−3, 2)
3o) x+3>x−2 i x∊<2, +∞)
Teraz rozwiązujesz te 3 przypadki − rozwiązaniem każdego przypadku jest część wspólna
rozwiązania nierówności i założenia.
ad 1o)
−x−3>−x+2 i x∊(−∞, −3)
−x+x>2+3
0>5 ⇒ sprzeczność ⇔ x∊∅
ad 2o)
x+3>−x+2 i x∊<−3, 2)
x+x>2−3
2x>−1 /:2
|x + 3| > |x −2|
Jak są dwa (i więcej) modułów, to wyznaczam miejsca zerowe każdego modułu i otrzymuję:
x=−3 i x=2
Potem metoda "osi i tabelki" − korzystasz z faktu, że każde wyrażenie typu x−a jest ujemne na
lewo od swojego miejsca zerowego (zaznaczyłem czerwoną linią), a dodanie na prawo od
niego. A więc na lewo od miejsca zerowego moduł danego wyrażenia opuszczamy ze zmianą znaku, a
na prawo − bez zmiany znaku.
Z osi i tabelki łatwiej sie odczytuje − metoda przyjazna dla wzroku, uczeń po prostu widzi, co
robi − łatwiej jest ułożyć przypadki.
Teraz jedziesz "kolumnami", a założeniami są przedziały zaznaczone nad daną kolumną:
1o) −x−3>−x+2 i x∊(−∞, −3)
2o) x+3>−x+2 i x∊<−3, 2)
3o) x+3>x−2 i x∊<2, +∞)
Teraz rozwiązujesz te 3 przypadki − rozwiązaniem każdego przypadku jest część wspólna
rozwiązania nierówności i założenia.
ad 1o)
−x−3>−x+2 i x∊(−∞, −3)
−x+x>2+3
0>5 ⇒ sprzeczność ⇔ x∊∅
ad 2o)
x+3>−x+2 i x∊<−3, 2)
x+x>2−3
2x>−1 /:2

 dla pigora
dla pigora 
 PW, ja też nie lubie podziału na przedziały, ale tego robionego "szkolną" metodą. Dlatego
opracowałem metodę "osi i tabelki" bo z tego te przedziały i przypadki się bardzo szybko
odczytuje, a tabelka nie jest skomplikowana.
Korzystam z "graficznej" interpretacji definicji wartości bezwzględnej, zamiast sie rozpisywać,
że
|x−a|={x−a, gdy x−a≥0⇔x≥a
{−x+a, gdy x−a<0⇔x<a
to rozrysowałem to sobie w sposób przedstawiony na rysunku i na lewo od miejsca zerowego takie
wyrażenie (x−a) jest ujemne, więc tam opuszczam moduł ze zmianą znaku, a na prawo od miejsca
zerowego wyrażenie (x−a) jest dodatnie, więc opuszczam moduł bez zmiany znaku, a założenia
odczytuje z przedziałów.
Stąd metoda "osi i tabelki", którą polecam, bo jest pzrejrzysta.
Pozdrawiam
PW, ja też nie lubie podziału na przedziały, ale tego robionego "szkolną" metodą. Dlatego
opracowałem metodę "osi i tabelki" bo z tego te przedziały i przypadki się bardzo szybko
odczytuje, a tabelka nie jest skomplikowana.
Korzystam z "graficznej" interpretacji definicji wartości bezwzględnej, zamiast sie rozpisywać,
że
|x−a|={x−a, gdy x−a≥0⇔x≥a
{−x+a, gdy x−a<0⇔x<a
to rozrysowałem to sobie w sposób przedstawiony na rysunku i na lewo od miejsca zerowego takie
wyrażenie (x−a) jest ujemne, więc tam opuszczam moduł ze zmianą znaku, a na prawo od miejsca
zerowego wyrażenie (x−a) jest dodatnie, więc opuszczam moduł bez zmiany znaku, a założenia
odczytuje z przedziałów.
Stąd metoda "osi i tabelki", którą polecam, bo jest pzrejrzysta.
Pozdrawiam 