POMOCY! BŁAGAM ! bezradny: W trójkącie ABC, w którym kąt A jest prosty, kreślimy koło styczne do boków BC i AC, mające środek na boku AB. Koło to przecina bok AB w punkcie M i jest styczne do przeciwprostokątnej w punkcie D. Wykaż, że jeżeli na przedłużeniu boku AC odłożymy CE, |CE| = |AC|, to punkty M, E, D leżą na jednej prostej.

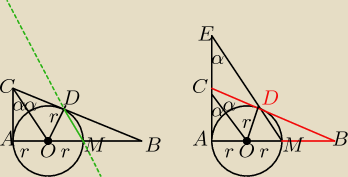
+-: kąt ABC=90−2α rys a kąt ODB=90 (styczna jest prostopadła do promienia)stąd kąt DOM=2α ΔDOM jest równoramienny OD=OM=r stąd kąty ODM=OMD=(180−2α)/2=90−α rys a ΔAOC oraz ΔAME są podobne posiadają kąt prosty, a ich dwa boki są w stosunku 1:2 (wynika z treści zadnia), tym samym ich kąty są odpowiednio równe, czyli AME=90−α jak zostało wykazane ocinki MD i ME wychodzące z tego samego punktu M są są nachylone do odcinka AM pod jednakowym kątem 90−α, a więc muszą leżeć na tej samej prostej, czyli punkt D równiez jako przynależny do odcinka MD,cnw.