
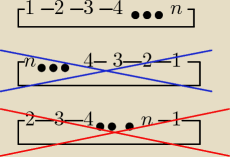
 Normalnie n osób tworzyłoby ciąg, który można ustawić na 6! sposobów.
Odwrócić kolejności nie możemy, ponieważ sąsiedzi się nie zmienią (niebieski), przez co o
połowę zmniejsza się ilość mozliwości.
Normalnie ciąg można przesuwać w ten sposób, że pierwszy przeskakuje na ostatnie miejsce, drugi
na pierwsze, i tak n razy. W przypadku kółka (czerwony) nie możemy tego zrobić, bo nic
nam się nie zmienia w kolejności (koło nie ma początku, ni końca). Tak więc ilość możliwości
spada nam n razy.
Zatem
Normalnie n osób tworzyłoby ciąg, który można ustawić na 6! sposobów.
Odwrócić kolejności nie możemy, ponieważ sąsiedzi się nie zmienią (niebieski), przez co o
połowę zmniejsza się ilość mozliwości.
Normalnie ciąg można przesuwać w ten sposób, że pierwszy przeskakuje na ostatnie miejsce, drugi
na pierwsze, i tak n razy. W przypadku kółka (czerwony) nie możemy tego zrobić, bo nic
nam się nie zmienia w kolejności (koło nie ma początku, ni końca). Tak więc ilość możliwości
spada nam n razy.
Zatem
| n! | ||
|A| = | ||
| 2n |